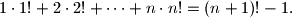Školjka Točno
19. siječnja 2016. 18:29 (8 godine, 3 mjeseci)
vrijedi 
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Dokaz provodimo matematickom indukcijom.
Baza indukcije:
Za n=1, tvrdnja vrijedi jer je 1*1!=(1+1)!-1, tj. 1=1.
Pretpostavka indukcije:
Pretpostavimo da za neki prirodni broj n vrijedi 1*1!+2*2!+....+n*n!=(n+1)! -1
Korak indukcije:
Onda trebamo dokazati da tvrdnja vrijedi i za n+1, tj. da vrijedi: 1*1!+2*2!+....n*n!+(n+1)*(n+1)!=(n+2)! -1
Koristeci pretpostavku indukcije dobivamo:
(n+1)!-1+(n+1)*(n+1)! = (n+1)!(1+n+1)-1 = (n+1)!(n+2)-1 = (n+2)!-1
Sto smo htjeli i dokazati.
Baza indukcije:
Za n=1, tvrdnja vrijedi jer je 1*1!=(1+1)!-1, tj. 1=1.
Pretpostavka indukcije:
Pretpostavimo da za neki prirodni broj n vrijedi 1*1!+2*2!+....+n*n!=(n+1)! -1
Korak indukcije:
Onda trebamo dokazati da tvrdnja vrijedi i za n+1, tj. da vrijedi: 1*1!+2*2!+....n*n!+(n+1)*(n+1)!=(n+2)! -1
Koristeci pretpostavku indukcije dobivamo:
(n+1)!-1+(n+1)*(n+1)! = (n+1)!(1+n+1)-1 = (n+1)!(n+2)-1 = (n+2)!-1
Sto smo htjeli i dokazati.