Točno
19. siječnja 2016. 23:26 (10 godine)
Korisnik: matsimic
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 3. (Sakrij tekst zadatka)
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 3. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (2)
Komentari:
ikicic, 19. siječnja 2016. 23:48
matsimic, 19. siječnja 2016. 23:46
Mislim, ono, semantika. "da bi postojalo rješenje, po tvrdnji zadatka mora postojati 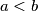 ..." Ali kužim šta hoćeš reći, te neke finese se izgube u notaciji.
..." Ali kužim šta hoćeš reći, te neke finese se izgube u notaciji.
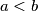 ..." Ali kužim šta hoćeš reći, te neke finese se izgube u notaciji.
..." Ali kužim šta hoćeš reći, te neke finese se izgube u notaciji.da ma ok. nije nis bitno, stvar je samo u zapisu, skuzi se sta si mislio.
iako bas taj dio sa "budući da mora postojati po tvrdnji zadatka" mi nije skroz 100%. obicno kad vidim ovakav zadatak nebih nuzno pretpostavio da rjesenje mora postojati. zapravo, prilicno sam siguran da ako je zadatak "nadi sve brojeve/parove brojeva/skupove/... tako da nesto" da moze biti da je rjesenje "ne postoji nijedan takav broj/par brojeva/skup/..."
iako bas taj dio sa "budući da mora postojati po tvrdnji zadatka" mi nije skroz 100%. obicno kad vidim ovakav zadatak nebih nuzno pretpostavio da rjesenje mora postojati. zapravo, prilicno sam siguran da ako je zadatak "nadi sve brojeve/parove brojeva/skupove/... tako da nesto" da moze biti da je rjesenje "ne postoji nijedan takav broj/par brojeva/skup/..."
U onom sam više mislio "budući da mora postojati po tvrdnji zadatka" nego tvrdio da postoji.
Hvala :D
Hvala :D
grga, 19. siječnja 2016. 23:44
da ma ok. nije nis bitno, stvar je samo u zapisu, skuzi se sta si mislio.
iako bas taj dio sa "budući da mora postojati po tvrdnji zadatka" mi nije skroz 100%. obicno kad vidim ovakav zadatak nebih nuzno pretpostavio da rjesenje mora postojati. zapravo, prilicno sam siguran da ako je zadatak "nadi sve brojeve/parove brojeva/skupove/... tako da nesto" da moze biti da je rjesenje "ne postoji nijedan takav broj/par brojeva/skup/..."
iako bas taj dio sa "budući da mora postojati po tvrdnji zadatka" mi nije skroz 100%. obicno kad vidim ovakav zadatak nebih nuzno pretpostavio da rjesenje mora postojati. zapravo, prilicno sam siguran da ako je zadatak "nadi sve brojeve/parove brojeva/skupove/... tako da nesto" da moze biti da je rjesenje "ne postoji nijedan takav broj/par brojeva/skup/..."
U onom sam više mislio "budući da mora postojati po tvrdnji zadatka" nego tvrdio da postoji.
Hvala :D
Hvala :D
grga, 19. siječnja 2016. 23:35
ikicic, 19. siječnja 2016. 23:31
 Školjka
Školjka 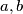 ,
, 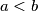 , takve da za sve realne brojeve
, takve da za sve realne brojeve ![x,y\in[a,b]](/media/m/1/0/e/10eecd0a7becb8f46e40e628617729df.png) vrijedi
vrijedi![\frac{1}{x}+\frac{1}{y}\in[a,b].](/media/m/c/3/1/c311e45b444da431a5bca5874bb927ef.png)
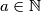 mora vrijediti
mora vrijediti 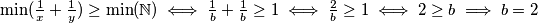 jer
jer 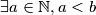 pa
pa 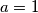
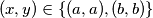 dobivamo da
dobivamo da 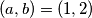 uistinu jest rješenje.
uistinu jest rješenje. 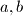 je
je 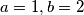 ". jer nitko ne kaze da takav
". jer nitko ne kaze da takav  postoji, zar ne? mislim da opcenito kad zadatak kaze "nadi sve
postoji, zar ne? mislim da opcenito kad zadatak kaze "nadi sve  tako da blabla.." moze se desit da nema rjesenja uopce.
tako da blabla.." moze se desit da nema rjesenja uopce. ![[1, 1]](/media/m/c/d/9/cd9d1a7a949d22a57d9da0bfed2abe13.png) sasvim dobro definiran.
sasvim dobro definiran.