Točno
22. siječnja 2016. 18:32 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 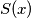 zbroj znamenaka broja
zbroj znamenaka broja  . Pod kongruencijom uvijek se misli
. Pod kongruencijom uvijek se misli 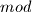
 .
.
Pri dodavanju broju njegov
broju njegov  se poveća za
se poveća za  , te se može oduzeti višekratnik
, te se može oduzeti višekratnik  ako neka devetka prelazi u nulu. Nazovimo to retardacijom.
ako neka devetka prelazi u nulu. Nazovimo to retardacijom.
Primijetimo nekoliko stvari: barem jedna retardacija će se sigurno dogoditi, mogu i dvije (ali ćemo to zanemariti jer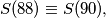
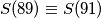 ).
).
Ukupno povećanje je pa retardacija mora biti barem
pa retardacija mora biti barem 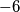 inače nalijećemo na
inače nalijećemo na 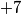 (promjene
(promjene 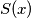 ). Prva takva je
). Prva takva je 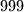 u
u 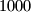 (
(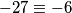 ).
).
Dolaze u obzir brojevi od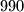 do
do 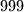 . Jedino nam odgovara sretni broj
. Jedino nam odgovara sretni broj 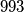 , koji je doista supersretan.
, koji je doista supersretan.
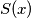 zbroj znamenaka broja
zbroj znamenaka broja  . Pod kongruencijom uvijek se misli
. Pod kongruencijom uvijek se misli 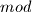
 .
.Pri dodavanju
 broju njegov
broju njegov  se poveća za
se poveća za  , te se može oduzeti višekratnik
, te se može oduzeti višekratnik  ako neka devetka prelazi u nulu. Nazovimo to retardacijom.
ako neka devetka prelazi u nulu. Nazovimo to retardacijom. Primijetimo nekoliko stvari: barem jedna retardacija će se sigurno dogoditi, mogu i dvije (ali ćemo to zanemariti jer
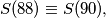
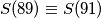 ).
).Ukupno povećanje je
 pa retardacija mora biti barem
pa retardacija mora biti barem 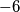 inače nalijećemo na
inače nalijećemo na 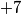 (promjene
(promjene 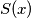 ). Prva takva je
). Prva takva je 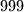 u
u 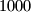 (
(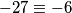 ).
). Dolaze u obzir brojevi od
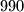 do
do 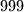 . Jedino nam odgovara sretni broj
. Jedino nam odgovara sretni broj 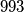 , koji je doista supersretan.
, koji je doista supersretan. Ocjene: (1)
Komentari:
rhldj, 27. siječnja 2016. 22:26
Daniel_Sirola, 27. siječnja 2016. 20:30
rhldj, 27. siječnja 2016. 19:45
Daniel_Sirola, 26. siječnja 2016. 09:28
Daniel_Sirola, 26. siječnja 2016. 09:27
ikicic, 23. siječnja 2016. 16:42
Više manje je dobro, ali neke stvari su čudne. Tipa, treći red ti ne treba (za dvostruku retardaciju), jer četvrti objašnjava cijelu poantu traženog rješenja. Na kraju, zašto dolaze u obzir brojevi od 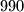 do
do 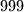 ? Četvrti red ti opet objašnjava u točno kojem trenutku se mora dogoditi retardacija. Znaš da
? Četvrti red ti opet objašnjava u točno kojem trenutku se mora dogoditi retardacija. Znaš da 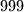 mora imati ostatak
mora imati ostatak  kako bi
kako bi 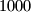 imao ponovno
imao ponovno  , dakle
, dakle 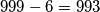 je rješenje.
je rješenje.
(kada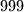 ne bi davao ostatak
ne bi davao ostatak  , morao bi ići na veće brojeve koji završavaju s
, morao bi ići na veće brojeve koji završavaju s 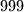 )
)
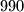 do
do 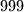 ? Četvrti red ti opet objašnjava u točno kojem trenutku se mora dogoditi retardacija. Znaš da
? Četvrti red ti opet objašnjava u točno kojem trenutku se mora dogoditi retardacija. Znaš da 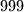 mora imati ostatak
mora imati ostatak  kako bi
kako bi 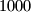 imao ponovno
imao ponovno  , dakle
, dakle 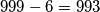 je rješenje.
je rješenje.(kada
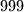 ne bi davao ostatak
ne bi davao ostatak  , morao bi ići na veće brojeve koji završavaju s
, morao bi ići na veće brojeve koji završavaju s 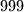 )
) Zadnja promjena: ikicic, 26. siječnja 2016. 10:36
 Školjka
Školjka  "sretan" ako mu je zbroj svih znamenaka višekratnik od
"sretan" ako mu je zbroj svih znamenaka višekratnik od 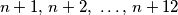 nije "sretan". Koji je najmanji "supersretan" prirodan broj?
nije "sretan". Koji je najmanji "supersretan" prirodan broj?