Točno
23. siječnja 2016. 08:57 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su  i
i  redom polovišta dužina
redom polovišta dužina  i
i  . Primijetimo:
. Primijetimo:  što stoji zbog
što stoji zbog 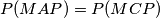 i
i 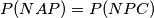 s obzirom da je
s obzirom da je  polovište
polovište  pa su
pa su 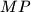 i
i 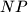 težišnice.
težišnice.
Dokazat ćemo dakle ekvivalentnu tvdnju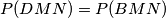 . Trokuti već imaju zajedničku
. Trokuti već imaju zajedničku  pa preostaje dokazati da su visine na istu jednake. Neka je
pa preostaje dokazati da su visine na istu jednake. Neka je  nožište visine iz
nožište visine iz  , a
, a  iz
iz  . Oba trokuta su pravokutna i imaju zajednički kut
. Oba trokuta su pravokutna i imaju zajednički kut
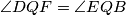 . Dva su kuta ista, pa su svi kutovi isti. Po definiciji polovišta je
. Dva su kuta ista, pa su svi kutovi isti. Po definiciji polovišta je 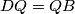 pa po
pa po 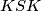 poučku slijedi
poučku slijedi 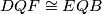 odnosno
odnosno 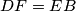 .
.
 i
i  redom polovišta dužina
redom polovišta dužina  i
i  . Primijetimo:
. Primijetimo:  što stoji zbog
što stoji zbog 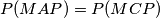 i
i 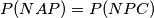 s obzirom da je
s obzirom da je  polovište
polovište  pa su
pa su 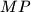 i
i 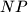 težišnice.
težišnice.Dokazat ćemo dakle ekvivalentnu tvdnju
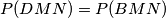 . Trokuti već imaju zajedničku
. Trokuti već imaju zajedničku  pa preostaje dokazati da su visine na istu jednake. Neka je
pa preostaje dokazati da su visine na istu jednake. Neka je  nožište visine iz
nožište visine iz  , a
, a  iz
iz  . Oba trokuta su pravokutna i imaju zajednički kut
. Oba trokuta su pravokutna i imaju zajednički kut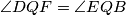 . Dva su kuta ista, pa su svi kutovi isti. Po definiciji polovišta je
. Dva su kuta ista, pa su svi kutovi isti. Po definiciji polovišta je 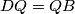 pa po
pa po 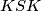 poučku slijedi
poučku slijedi 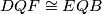 odnosno
odnosno 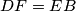 .
. Ocjene: (1)
Komentari:
grga, 1. ožujka 2016. 01:59
tocno, ali donekle cudno.
ovaj prvi dio "što stoji zbog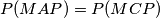 i
i 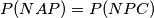 " zapravo kaze
" zapravo kaze 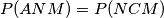 .
.
sad mozes posve analogno pokazat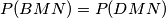 , ne moras ici na ove visine kako si krenuo u drugom dijelu dokaza.
, ne moras ici na ove visine kako si krenuo u drugom dijelu dokaza.
ili si mogao onda i tu prvu jednakost povrsina dokazat analogno, preko visina.
ne kazem da je ovo lose, sto vise, dao si 2 donekle razlicita pricipa za dokazati istu stvar, al mislim da se na natjecanjima isplati uocavat ovakve "simetrije" u zadacima jer zna bitno skratiti postupak i ne moras smisljati novo rjesenje nego samo "prepises" ono prvo ili naprosto napises "analogno se vidi" i nadas se da ti nece skinut puno bodova na tome :)
ovaj prvi dio "što stoji zbog
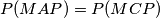 i
i 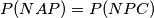 " zapravo kaze
" zapravo kaze 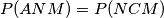 .
.sad mozes posve analogno pokazat
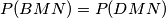 , ne moras ici na ove visine kako si krenuo u drugom dijelu dokaza.
, ne moras ici na ove visine kako si krenuo u drugom dijelu dokaza.ili si mogao onda i tu prvu jednakost povrsina dokazat analogno, preko visina.
ne kazem da je ovo lose, sto vise, dao si 2 donekle razlicita pricipa za dokazati istu stvar, al mislim da se na natjecanjima isplati uocavat ovakve "simetrije" u zadacima jer zna bitno skratiti postupak i ne moras smisljati novo rjesenje nego samo "prepises" ono prvo ili naprosto napises "analogno se vidi" i nadas se da ti nece skinut puno bodova na tome :)
 Školjka
Školjka  koji nije paralelogram. Neka pravac koji prolazi kroz polovišta dijagonala četverokuta siječe stranice
koji nije paralelogram. Neka pravac koji prolazi kroz polovišta dijagonala četverokuta siječe stranice  i
i  redom u točkama
redom u točkama  i
i  . Dokaži da trokuti
. Dokaži da trokuti 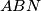 i
i 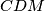 imaju jednake površine.
imaju jednake površine.