Točno
23. siječnja 2016. 09:50 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Oduzimanjem jednakosti se dobiva 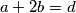 . Neka su onda katete
. Neka su onda katete  i
i  . Vrijedi
. Vrijedi 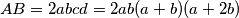 i
i 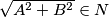 .
.
Organizirajmo sada i
i  tako da im je zbroj kvadrata kvadrat. Eksperimentiranjem s manjim brojevima čini se da je
tako da im je zbroj kvadrata kvadrat. Eksperimentiranjem s manjim brojevima čini se da je 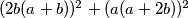 uvijek kvadrat.
uvijek kvadrat.
To je doista uvijek točno jer je izraz jednak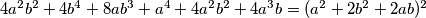 .
.
Dakle traženi trokut uvijek postoji i katete su mu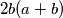 i
i 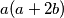 odnosno
odnosno 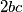 i
i 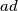 , a hipotenuza
, a hipotenuza 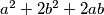 .
.
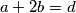 . Neka su onda katete
. Neka su onda katete  i
i  . Vrijedi
. Vrijedi 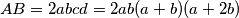 i
i 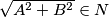 .
.Organizirajmo sada
 i
i  tako da im je zbroj kvadrata kvadrat. Eksperimentiranjem s manjim brojevima čini se da je
tako da im je zbroj kvadrata kvadrat. Eksperimentiranjem s manjim brojevima čini se da je 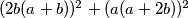 uvijek kvadrat.
uvijek kvadrat.To je doista uvijek točno jer je izraz jednak
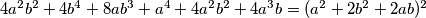 .
.Dakle traženi trokut uvijek postoji i katete su mu
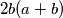 i
i 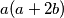 odnosno
odnosno 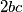 i
i 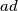 , a hipotenuza
, a hipotenuza 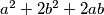 .
.  Školjka
Školjka  ,
,  ,
,  ,
,  zadovoljavaju jednakosti
zadovoljavaju jednakosti  Pokaži da postoji pravokutni trokut površine
Pokaži da postoji pravokutni trokut površine 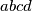 kojem su duljine svih stranica prirodni brojevi.
kojem su duljine svih stranica prirodni brojevi.