Točno
26. siječnja 2016. 20:39 (8 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Dana nejednakost je ekvivalentna s:
![\frac{\sqrt[3]{6ab+1}}{\sqrt[3]{a}}+\frac{\sqrt[3]{6bc+1}}{\sqrt[3]{b}}+\frac{\sqrt[3]{6ac+1}}{\sqrt[3]{c}}\leq\frac{1}{abc}](/media/m/c/4/b/c4ba1f5e916a1e50a96e584334f78d1b.png)
Odnosno nakon svođenja na zajednički nazivnik:
![\frac{\sqrt[3]{(6ab+1)bc}+\sqrt[3]{(6bc+1)ac}+\sqrt[3]{(6ac+1)ab}}{\sqrt[3]{abc}}\leq\frac{1}{abc}](/media/m/f/7/2/f72c3d3bcede5b8312ee13b7fe4735f4.png)
Sada kubiramo:
![[\sqrt[3]{(6ab+1)bc}+\sqrt[3]{(6bc+1)ac}+\sqrt[3]{(6ac+1)ab}]^3\leq\frac{1}{(abc)^2}](/media/m/0/f/7/0f7cbaea80c4f8335528c903a2868804.png)
I koristimo Holderovu nejednakost na lijevu stranu:
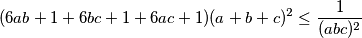
Množimo nejednakost s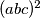 i zbog uvjeta zadatka preostaje dokazati:
i zbog uvjeta zadatka preostaje dokazati:
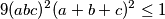
Ali iz uvjeta zadatka imamo i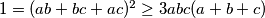 pa kada kvadriramo ovu nejednakost, dobivamo točno ono što je preostalo dokazati čime smo gotovi.
pa kada kvadriramo ovu nejednakost, dobivamo točno ono što je preostalo dokazati čime smo gotovi.
![\frac{\sqrt[3]{6ab+1}}{\sqrt[3]{a}}+\frac{\sqrt[3]{6bc+1}}{\sqrt[3]{b}}+\frac{\sqrt[3]{6ac+1}}{\sqrt[3]{c}}\leq\frac{1}{abc}](/media/m/c/4/b/c4ba1f5e916a1e50a96e584334f78d1b.png)
Odnosno nakon svođenja na zajednički nazivnik:
![\frac{\sqrt[3]{(6ab+1)bc}+\sqrt[3]{(6bc+1)ac}+\sqrt[3]{(6ac+1)ab}}{\sqrt[3]{abc}}\leq\frac{1}{abc}](/media/m/f/7/2/f72c3d3bcede5b8312ee13b7fe4735f4.png)
Sada kubiramo:
![[\sqrt[3]{(6ab+1)bc}+\sqrt[3]{(6bc+1)ac}+\sqrt[3]{(6ac+1)ab}]^3\leq\frac{1}{(abc)^2}](/media/m/0/f/7/0f7cbaea80c4f8335528c903a2868804.png)
I koristimo Holderovu nejednakost na lijevu stranu:
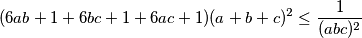
Množimo nejednakost s
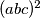 i zbog uvjeta zadatka preostaje dokazati:
i zbog uvjeta zadatka preostaje dokazati: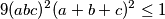
Ali iz uvjeta zadatka imamo i
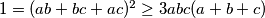 pa kada kvadriramo ovu nejednakost, dobivamo točno ono što je preostalo dokazati čime smo gotovi.
pa kada kvadriramo ovu nejednakost, dobivamo točno ono što je preostalo dokazati čime smo gotovi. Ocjene: (2)
Komentari:
ikicic, 27. siječnja 2016. 11:52
Aha, da, nije komplicirano. Hvala!
Najednostavije je ab = x, bc = y, ca = z, pa nejednakost jednostavno postane : (x + y + z)^2 >= 3(xy + yz + zx)
Kako se najjednostavnije pokaže zadnja tvrdnja 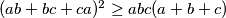 ?
?
Pretpostavljam da postoji nešto očito, ali ne pada mi na pamet ništa osim raspisivanja i A-G po dijelovima.
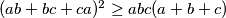 ?
?Pretpostavljam da postoji nešto očito, ali ne pada mi na pamet ništa osim raspisivanja i A-G po dijelovima.
leonstaresinic, 27. siječnja 2016. 09:43
ikicic, 27. siječnja 2016. 01:36
grga, 26. siječnja 2016. 21:49
 Školjka
Školjka  are three positive real numbers such that
are three positive real numbers such that 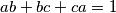 , prove that
, prove that ![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
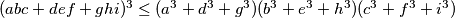 pa stavljam ovdje ako jos neko zapne citajuci taj korak.
pa stavljam ovdje ako jos neko zapne citajuci taj korak.