Točno
6. ožujka 2016. 14:39 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Nije moguće odabrati 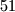 brojeva s tim svojstvom (onda naravno ni više).
brojeva s tim svojstvom (onda naravno ni više).
Dokaz:
Brojeve podijelimo u skupova:
skupova: 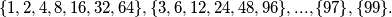 (neparan broj iz skupa te njegovi produkti s potencijama broja 2 iz skupa).
(neparan broj iz skupa te njegovi produkti s potencijama broja 2 iz skupa).
Imamo skupova, a
skupova, a 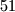 broj pa slijedi da postoje dva broja iz istog skupa, odnosno jedan dijeli drugog (Dirichletov princip).
broj pa slijedi da postoje dva broja iz istog skupa, odnosno jedan dijeli drugog (Dirichletov princip).
S druge strane, brojeva je moguće odabrati,
brojeva je moguće odabrati, 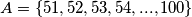 . Dakle,
. Dakle,  .
.
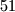 brojeva s tim svojstvom (onda naravno ni više).
brojeva s tim svojstvom (onda naravno ni više).Dokaz:
Brojeve podijelimo u
 skupova:
skupova: 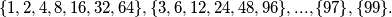 (neparan broj iz skupa te njegovi produkti s potencijama broja 2 iz skupa).
(neparan broj iz skupa te njegovi produkti s potencijama broja 2 iz skupa).Imamo
 skupova, a
skupova, a 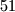 broj pa slijedi da postoje dva broja iz istog skupa, odnosno jedan dijeli drugog (Dirichletov princip).
broj pa slijedi da postoje dva broja iz istog skupa, odnosno jedan dijeli drugog (Dirichletov princip).S druge strane,
 brojeva je moguće odabrati,
brojeva je moguće odabrati, 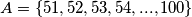 . Dakle,
. Dakle,  .
.  Školjka
Školjka  najveći podskup od
najveći podskup od 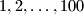 koji ne sadrži dva elementa takva da jedan dijeli drugog. Koliko je
koji ne sadrži dva elementa takva da jedan dijeli drugog. Koliko je 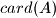 ?
?