Točno
1. veljače 2016. 21:15 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prvo prebacimo jedinicu na lijevu stranu:
![2\sqrt[3]{2x-1}-1=x^3](/media/m/f/a/e/fae3446abfc63afce1b5875e997d4576.png)
I sada primijetimo da se izraz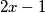 na neki način ponavlja na lijevoj strani, odnosno ako stavimo
na neki način ponavlja na lijevoj strani, odnosno ako stavimo 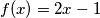 , početnu jednadžbu možemo zapisati kao:
, početnu jednadžbu možemo zapisati kao:
![f(\sqrt[3]{f(x)})=x^3](/media/m/4/f/8/4f87324c8340b59b4b65423b38e61523.png)
Sada bi nam bilo dobro naći funkciju koja zadovoljava ovu jednadžbu koju bismo onda izjednačili s izrazom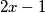 kako bi dobili neka rješenja dane jednakosti. Kako se u ovoj funkcijskoj jednadžbi samo vade korijeni i dižu potencije, dobra pretpostavka za oblik funkcije koja ovo zadovoljava je
kako bi dobili neka rješenja dane jednakosti. Kako se u ovoj funkcijskoj jednadžbi samo vade korijeni i dižu potencije, dobra pretpostavka za oblik funkcije koja ovo zadovoljava je 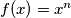 . Sada imamo:
. Sada imamo:
![(\sqrt[3]{x^n})^n=x^3](/media/m/3/7/1/371ddcb2b812c9f0f372a00c8936a4cb.png)
Odnosno:
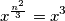
Iz čega dobivamo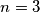 i funkcija
i funkcija 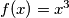 zadovoljava funkcijsku jednadžbu. Dakle svi brojevi
zadovoljava funkcijsku jednadžbu. Dakle svi brojevi  za koje vrijedi
za koje vrijedi 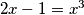 zadovoljavaju početnu jednadžbu pa njezina tri rješenja možemo naći rješavajući ovu kubnu jednadžbu (čije je jedno rješenje
zadovoljavaju početnu jednadžbu pa njezina tri rješenja možemo naći rješavajući ovu kubnu jednadžbu (čije je jedno rješenje  što olakšava posao). Ta tri rješenja su
što olakšava posao). Ta tri rješenja su 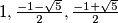 . Na početku rješavanja zadatka mogli smo kubirati danu jednadžbu što bi nas dovelo do nalaženja nultočaka polinoma
. Na početku rješavanja zadatka mogli smo kubirati danu jednadžbu što bi nas dovelo do nalaženja nultočaka polinoma 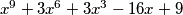 i to nije jednostavan zadatak, međutim sada kad znamo tri njegove nultočke možemo ga podijeliti polinomom
i to nije jednostavan zadatak, međutim sada kad znamo tri njegove nultočke možemo ga podijeliti polinomom 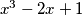 da bi dobili polinom manjeg stupnja. Taj polinom je:
da bi dobili polinom manjeg stupnja. Taj polinom je:
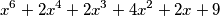
Naš je zadatak sada naći njegove realne korijene, odnosno u ovom slučaju pokazati da ih nema.
Ako je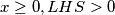 i tu nemamo rješenja.
i tu nemamo rješenja.
Ako je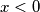 , članovi
, članovi 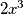 i
i 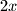 su negativni dok su ostali pozitivni pa stavimo li
su negativni dok su ostali pozitivni pa stavimo li 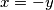 potrebno je dokazati:
potrebno je dokazati:
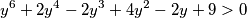
Ali to se može zapisati kao:
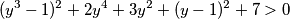
Što sigurno vrijedi i time smo dokazali da početna jednadžba ima samo tri rješenja: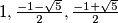 .
.
![2\sqrt[3]{2x-1}-1=x^3](/media/m/f/a/e/fae3446abfc63afce1b5875e997d4576.png)
I sada primijetimo da se izraz
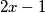 na neki način ponavlja na lijevoj strani, odnosno ako stavimo
na neki način ponavlja na lijevoj strani, odnosno ako stavimo 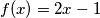 , početnu jednadžbu možemo zapisati kao:
, početnu jednadžbu možemo zapisati kao:![f(\sqrt[3]{f(x)})=x^3](/media/m/4/f/8/4f87324c8340b59b4b65423b38e61523.png)
Sada bi nam bilo dobro naći funkciju koja zadovoljava ovu jednadžbu koju bismo onda izjednačili s izrazom
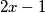 kako bi dobili neka rješenja dane jednakosti. Kako se u ovoj funkcijskoj jednadžbi samo vade korijeni i dižu potencije, dobra pretpostavka za oblik funkcije koja ovo zadovoljava je
kako bi dobili neka rješenja dane jednakosti. Kako se u ovoj funkcijskoj jednadžbi samo vade korijeni i dižu potencije, dobra pretpostavka za oblik funkcije koja ovo zadovoljava je 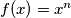 . Sada imamo:
. Sada imamo:![(\sqrt[3]{x^n})^n=x^3](/media/m/3/7/1/371ddcb2b812c9f0f372a00c8936a4cb.png)
Odnosno:
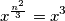
Iz čega dobivamo
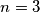 i funkcija
i funkcija 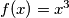 zadovoljava funkcijsku jednadžbu. Dakle svi brojevi
zadovoljava funkcijsku jednadžbu. Dakle svi brojevi  za koje vrijedi
za koje vrijedi 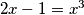 zadovoljavaju početnu jednadžbu pa njezina tri rješenja možemo naći rješavajući ovu kubnu jednadžbu (čije je jedno rješenje
zadovoljavaju početnu jednadžbu pa njezina tri rješenja možemo naći rješavajući ovu kubnu jednadžbu (čije je jedno rješenje  što olakšava posao). Ta tri rješenja su
što olakšava posao). Ta tri rješenja su 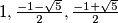 . Na početku rješavanja zadatka mogli smo kubirati danu jednadžbu što bi nas dovelo do nalaženja nultočaka polinoma
. Na početku rješavanja zadatka mogli smo kubirati danu jednadžbu što bi nas dovelo do nalaženja nultočaka polinoma 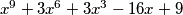 i to nije jednostavan zadatak, međutim sada kad znamo tri njegove nultočke možemo ga podijeliti polinomom
i to nije jednostavan zadatak, međutim sada kad znamo tri njegove nultočke možemo ga podijeliti polinomom 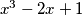 da bi dobili polinom manjeg stupnja. Taj polinom je:
da bi dobili polinom manjeg stupnja. Taj polinom je: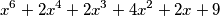
Naš je zadatak sada naći njegove realne korijene, odnosno u ovom slučaju pokazati da ih nema.
Ako je
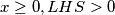 i tu nemamo rješenja.
i tu nemamo rješenja.Ako je
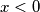 , članovi
, članovi 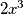 i
i 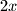 su negativni dok su ostali pozitivni pa stavimo li
su negativni dok su ostali pozitivni pa stavimo li 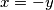 potrebno je dokazati:
potrebno je dokazati: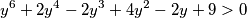
Ali to se može zapisati kao:
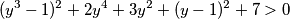
Što sigurno vrijedi i time smo dokazali da početna jednadžba ima samo tri rješenja:
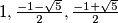 .
.  Školjka
Školjka 
![2\sqrt[3]{2x-1} = x^3+1](/media/m/e/6/6/e66a43a64b18d2e4cc8dfd8c390d292f.png)