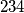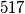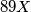Točno
18. veljače 2016. 21:26 (10 godine)
Korisnik: matsimic
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
grga, 21. veljače 2016. 21:03
 Školjka
Školjka 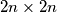 upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem
upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem 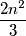 puta.
puta.  polja tablice.
polja tablice.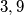 također nisu susjedni, oni zauzimaju najviše
također nisu susjedni, oni zauzimaju najviše 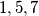 zauzimaju najmanje
zauzimaju najmanje  polja.
polja.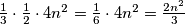 polja.
polja. 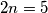 mozes imati nesto tipa (sori na nepreglednoj tablici neda mi se sad traziti kak se lijepo radi)
mozes imati nesto tipa (sori na nepreglednoj tablici neda mi se sad traziti kak se lijepo radi)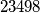
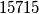
 i
i  pojavljuju najvise,
pojavljuju najvise,  puta, a
puta, a 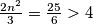 .
.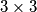 tablicu lose:
tablicu lose: