Točno
21. ožujka 2016. 17:20 (9 godine, 11 mjeseci)
Korisnik: rhldj
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
grga, 21. veljače 2016. 20:54
sad si dokazao da je izraz uvijek 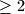 , ali ako tražiš minimum moras naci i slucaj kad se ta vrijednost postize. jer ono, mogu ja dosta lako pokazat da je taj izraz
, ali ako tražiš minimum moras naci i slucaj kad se ta vrijednost postize. jer ono, mogu ja dosta lako pokazat da je taj izraz 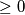 , pa ne znaci da je to minimum. ok, ovdje je to trivijalno tipa kad je
, pa ne znaci da je to minimum. ok, ovdje je to trivijalno tipa kad je 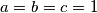 , al opet takve stvari bi trebao pisati. inace je takoder interesantno da se minimum uopce ne mora postizati. npr ako imas "uvjet
, al opet takve stvari bi trebao pisati. inace je takoder interesantno da se minimum uopce ne mora postizati. npr ako imas "uvjet 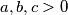 , nadi minimum od
, nadi minimum od 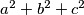 " .. ok sad je glup primjer, al jasno da je ovaj izraz uvijek
" .. ok sad je glup primjer, al jasno da je ovaj izraz uvijek 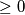 , ali da se
, ali da se  nikada nece postici. to se onda zove infimum, cisto ako ce neko htjeti guglati malo.
nikada nece postici. to se onda zove infimum, cisto ako ce neko htjeti guglati malo.
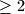 , ali ako tražiš minimum moras naci i slucaj kad se ta vrijednost postize. jer ono, mogu ja dosta lako pokazat da je taj izraz
, ali ako tražiš minimum moras naci i slucaj kad se ta vrijednost postize. jer ono, mogu ja dosta lako pokazat da je taj izraz 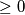 , pa ne znaci da je to minimum. ok, ovdje je to trivijalno tipa kad je
, pa ne znaci da je to minimum. ok, ovdje je to trivijalno tipa kad je 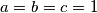 , al opet takve stvari bi trebao pisati. inace je takoder interesantno da se minimum uopce ne mora postizati. npr ako imas "uvjet
, al opet takve stvari bi trebao pisati. inace je takoder interesantno da se minimum uopce ne mora postizati. npr ako imas "uvjet 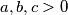 , nadi minimum od
, nadi minimum od 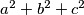 " .. ok sad je glup primjer, al jasno da je ovaj izraz uvijek
" .. ok sad je glup primjer, al jasno da je ovaj izraz uvijek 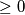 , ali da se
, ali da se  nikada nece postici. to se onda zove infimum, cisto ako ce neko htjeti guglati malo.
nikada nece postici. to se onda zove infimum, cisto ako ce neko htjeti guglati malo. dpaleka, 19. veljače 2016. 20:07
 Školjka
Školjka  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 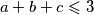 . Odredite najmanju moguću vrijednost izraza
. Odredite najmanju moguću vrijednost izraza 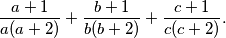
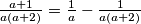 , ali i
, ali i 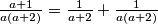 . Kad zbrojimo jednakosti, dobivamo
. Kad zbrojimo jednakosti, dobivamo 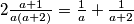 .
.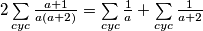 .
.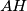 vrijedi da je
vrijedi da je 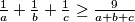 .
.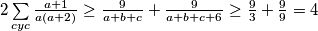 , odnosno
, odnosno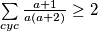 , što je traženi minimum.
, što je traženi minimum.