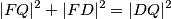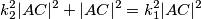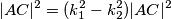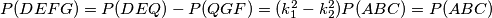Točno
22. veljače 2016. 08:49 (9 godine, 11 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
grga, 21. veljače 2016. 21:23
super rjesenje!
ipak samo par sitnica:
mislim da ti u je u definiciji zadnji razlomak okrenut.
zadnji razlomak okrenut.
mozda mozes razmislit sta ako je trokut jednakokracan, pa u zadnjem redu nemozes podijelit s nulom (tvrdnja bi morala vrijedit i dalje al mozda bi se moglo nekako lijepo argumentirati).
vidim da pazis da lijepo i formalno sve zapises sto je izuzetno pohvalno. zato sam mislio da ce te mozda ovo zanimati, al to stvarno nije neka greska. kad stavis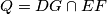 , zapravo trebas stavit
, zapravo trebas stavit 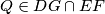 . jer po definiciji, pravac je skup tocaka, dakle malo neformalno:
. jer po definiciji, pravac je skup tocaka, dakle malo neformalno: 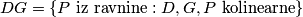 . zato je
. zato je 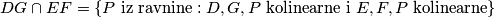 . sad, konkretnije mi znamo da je u slucaju dva pravca, njihov presjek najcesce jedna tocka, ako ju oznacimo s
. sad, konkretnije mi znamo da je u slucaju dva pravca, njihov presjek najcesce jedna tocka, ako ju oznacimo s  imamo:
imamo: 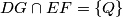 , pa je zato ispravnije pisati
, pa je zato ispravnije pisati 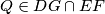 , nego
, nego 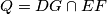 . naravno, na ovakvim stvarima ti na natjecanjima nebi smjeli skidat bodove (dapace, bas suprotno, jer ti je rjesenje stvarno lijepo napisano), al sam mislio da bi te moglo zanimat.
. naravno, na ovakvim stvarima ti na natjecanjima nebi smjeli skidat bodove (dapace, bas suprotno, jer ti je rjesenje stvarno lijepo napisano), al sam mislio da bi te moglo zanimat.
ipak samo par sitnica:
mislim da ti u je u definiciji
 zadnji razlomak okrenut.
zadnji razlomak okrenut.mozda mozes razmislit sta ako je trokut jednakokracan, pa u zadnjem redu nemozes podijelit s nulom (tvrdnja bi morala vrijedit i dalje al mozda bi se moglo nekako lijepo argumentirati).
vidim da pazis da lijepo i formalno sve zapises sto je izuzetno pohvalno. zato sam mislio da ce te mozda ovo zanimati, al to stvarno nije neka greska. kad stavis
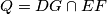 , zapravo trebas stavit
, zapravo trebas stavit 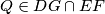 . jer po definiciji, pravac je skup tocaka, dakle malo neformalno:
. jer po definiciji, pravac je skup tocaka, dakle malo neformalno: 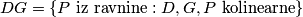 . zato je
. zato je 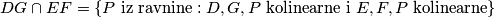 . sad, konkretnije mi znamo da je u slucaju dva pravca, njihov presjek najcesce jedna tocka, ako ju oznacimo s
. sad, konkretnije mi znamo da je u slucaju dva pravca, njihov presjek najcesce jedna tocka, ako ju oznacimo s  imamo:
imamo: 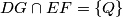 , pa je zato ispravnije pisati
, pa je zato ispravnije pisati 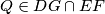 , nego
, nego 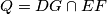 . naravno, na ovakvim stvarima ti na natjecanjima nebi smjeli skidat bodove (dapace, bas suprotno, jer ti je rjesenje stvarno lijepo napisano), al sam mislio da bi te moglo zanimat.
. naravno, na ovakvim stvarima ti na natjecanjima nebi smjeli skidat bodove (dapace, bas suprotno, jer ti je rjesenje stvarno lijepo napisano), al sam mislio da bi te moglo zanimat.  Školjka
Školjka  opisana je kružnica. Neka je
opisana je kružnica. Neka je 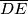 promjer te kružnice paralelan stranici
promjer te kružnice paralelan stranici  . Neka su
. Neka su 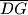 i
i 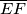 tetive paralelne drugim dvjema stranicama trokuta
tetive paralelne drugim dvjema stranicama trokuta 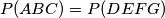 .
. 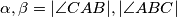 .
.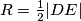
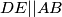 te
te 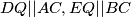 su
su 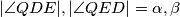 pa je
pa je 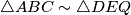 .
.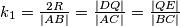 pa vrijedi i:
pa vrijedi i: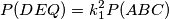
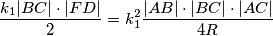
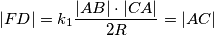
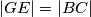 .
.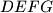 ,
, 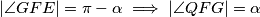 , analogno i
, analogno i 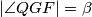 pa vrijedi
pa vrijedi 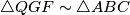 uz koeficijent
uz koeficijent 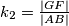
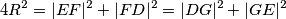
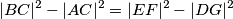
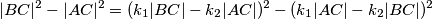
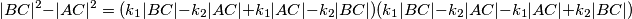
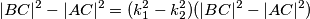
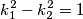
 jednakokračan, vrijedi:
jednakokračan, vrijedi: