Točno
2. travnja 2012. 21:51 (13 godine, 10 mjeseci)
Od svih brojeva oblika
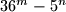
, gdje su

i

prirodni brojevi, odredi najmanji po apsolutnoj vrijednosti.
%V0
Od svih brojeva oblika $36^m - 5^n$, gdje su $m$ i $n$ prirodni brojevi, odredi najmanji po apsolutnoj vrijednosti.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
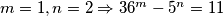
. pokazimo da je

minimalno. ili je vece
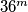
ili
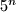
. takoder,
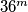
zavrsava sa

uvijek, a
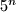
sa

.
a)
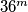
veci - moguce razlike su
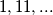
ako je razlika

onda
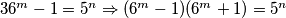
, ali buduci da je
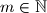
nije moguce da
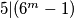
i
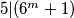
jer tada
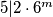
sto nije istina.
b)
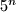
veci - moguce razlike su
ali

nemoze biti, jer

nije djeljivo s

%V0
$m = 1, n = 2 \Rightarrow 36^m - 5^n = 11$. pokazimo da je $11$ minimalno. ili je vece $36^m$ ili $5^n$. takoder, $36^m$ zavrsava sa $6$ uvijek, a $5^n$ sa $5$.
a) $36^m$ veci - moguce razlike su $1, 11, ...$
ako je razlika $1$ onda
$36^m - 1 = 5^n \Rightarrow (6^m - 1)(6^m + 1) = 5^n$, ali buduci da je $m \in \mathbb{N}$ nije moguce da $5 | (6^m - 1)$ i $5 | (6^m + 1)$ jer tada $5 | 2 \cdot 6^m$ sto nije istina.
b) $5^n$ veci - moguce razlike su $9, 19, ...$
ali $9$ nemoze biti, jer $5$ nije djeljivo s $3$