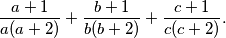Neocijenjeno
23. veljače 2016. 13:29 (10 godine)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vrijedi: 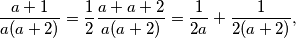 i potpuno analogno,
i potpuno analogno, 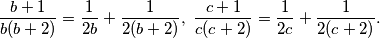 Primjenom
Primjenom 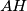 nejednakosti i uvjeta zadatka dobivamo
nejednakosti i uvjeta zadatka dobivamo 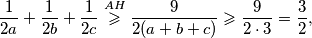
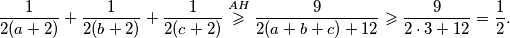 Zbrajanjem dobivenih nejednakosti i korištenjem gornjih identiteta slijedi
Zbrajanjem dobivenih nejednakosti i korištenjem gornjih identiteta slijedi 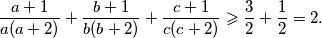 Uočimo da ovo uistinu jest najmanja moguća vrijednost zadanog izraza: naime, jednakost se postiže kada se postižu jednakosti u
Uočimo da ovo uistinu jest najmanja moguća vrijednost zadanog izraza: naime, jednakost se postiže kada se postižu jednakosti u  nejednakostima i u uvjetu zadatka, a to je u slučaju
nejednakostima i u uvjetu zadatka, a to je u slučaju 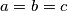 i
i 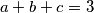 . Dakle, jednakost se postiže za
. Dakle, jednakost se postiže za 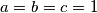 .
.
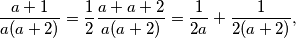 i potpuno analogno,
i potpuno analogno, 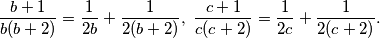 Primjenom
Primjenom 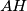 nejednakosti i uvjeta zadatka dobivamo
nejednakosti i uvjeta zadatka dobivamo 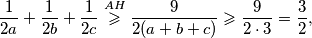
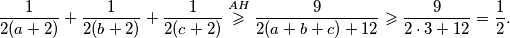 Zbrajanjem dobivenih nejednakosti i korištenjem gornjih identiteta slijedi
Zbrajanjem dobivenih nejednakosti i korištenjem gornjih identiteta slijedi 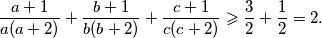 Uočimo da ovo uistinu jest najmanja moguća vrijednost zadanog izraza: naime, jednakost se postiže kada se postižu jednakosti u
Uočimo da ovo uistinu jest najmanja moguća vrijednost zadanog izraza: naime, jednakost se postiže kada se postižu jednakosti u 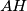 nejednakostima i u uvjetu zadatka, a to je u slučaju
nejednakostima i u uvjetu zadatka, a to je u slučaju 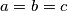 i
i 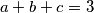 . Dakle, jednakost se postiže za
. Dakle, jednakost se postiže za 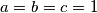 .
.  Školjka
Školjka  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 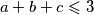 . Odredite najmanju moguću vrijednost izraza
. Odredite najmanju moguću vrijednost izraza