Točno
23. veljače 2016. 13:32 (10 godine)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Očito je 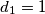 . Pretpostavimo da je
. Pretpostavimo da je  neparan. Tada u zadanoj jednakosti na lijevoj strani imamo zbroj četiri neparna broja (dakle, paran broj), a na desnoj neparan broj. Kontradikcija. Zato je
neparan. Tada u zadanoj jednakosti na lijevoj strani imamo zbroj četiri neparna broja (dakle, paran broj), a na desnoj neparan broj. Kontradikcija. Zato je  paran, pa je
paran, pa je 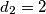 . Pretpostavimo da je
. Pretpostavimo da je 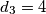 . Tada je
. Tada je 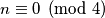 i
i 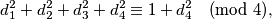 pa slijedi
pa slijedi 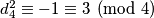 . No, kvadrat prirodnog broja može davati samo ostatke 0 i 1 pri dijeljenju s 4. Zato
. No, kvadrat prirodnog broja može davati samo ostatke 0 i 1 pri dijeljenju s 4. Zato 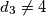 . Potpuno analogno dobijemo i
. Potpuno analogno dobijemo i 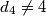 .
.
Iz prethodnog razmatranja zaključujemo kako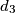 mora biti jednak nekom (neparnom) prostom broju
mora biti jednak nekom (neparnom) prostom broju  (u suprotnom bi, zbog
(u suprotnom bi, zbog 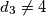 , slijedilo da
, slijedilo da 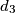 ima prost djelitelj veći od 2 pa
ima prost djelitelj veći od 2 pa 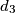 ne bi bio treći najmanji djelitelj od
ne bi bio treći najmanji djelitelj od  ). Sada imamo
). Sada imamo 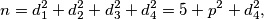 a budući da je
a budući da je  paran i
paran i  neparan, slijedi da
neparan, slijedi da 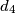 mora biti paran, tj.
mora biti paran, tj. 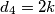 . Uočimo da
. Uočimo da  ima sve proste faktore veće ili jednake
ima sve proste faktore veće ili jednake  (u suprotnom
(u suprotnom  ne bi bio treći najmanji djelitelj od
ne bi bio treći najmanji djelitelj od  ). Pretpostavimo da
). Pretpostavimo da  ima prost djelitelj
ima prost djelitelj  koji je strogo veći od
koji je strogo veći od  (uočimo da
(uočimo da  mora biti neparan). Tada je
mora biti neparan). Tada je  djelitelj od
djelitelj od  koji je manji od
koji je manji od 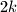 , pa bi četvrti najmanji djelitelj od
, pa bi četvrti najmanji djelitelj od  bio neparan. Kontradikcija, dakle,
bio neparan. Kontradikcija, dakle,  je jedini prost djelitelj od
je jedini prost djelitelj od  . Budući da je
. Budući da je 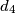 četvrti najmanji djelitelj od
četvrti najmanji djelitelj od  , slijedi
, slijedi 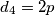 .
.
Dakle, imamo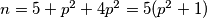 . Budući da
. Budući da  dijeli
dijeli  i
i  ne dijeli
ne dijeli 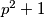 , vidimo da
, vidimo da  mora dijeliti
mora dijeliti  . Dakle,
. Dakle, 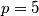 i
i 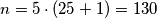 je jedini broj s traženim svojstvom.
je jedini broj s traženim svojstvom.
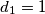 . Pretpostavimo da je
. Pretpostavimo da je  neparan. Tada u zadanoj jednakosti na lijevoj strani imamo zbroj četiri neparna broja (dakle, paran broj), a na desnoj neparan broj. Kontradikcija. Zato je
neparan. Tada u zadanoj jednakosti na lijevoj strani imamo zbroj četiri neparna broja (dakle, paran broj), a na desnoj neparan broj. Kontradikcija. Zato je  paran, pa je
paran, pa je 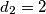 . Pretpostavimo da je
. Pretpostavimo da je 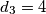 . Tada je
. Tada je 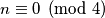 i
i 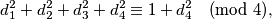 pa slijedi
pa slijedi 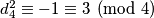 . No, kvadrat prirodnog broja može davati samo ostatke 0 i 1 pri dijeljenju s 4. Zato
. No, kvadrat prirodnog broja može davati samo ostatke 0 i 1 pri dijeljenju s 4. Zato 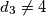 . Potpuno analogno dobijemo i
. Potpuno analogno dobijemo i 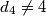 .
.Iz prethodnog razmatranja zaključujemo kako
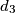 mora biti jednak nekom (neparnom) prostom broju
mora biti jednak nekom (neparnom) prostom broju  (u suprotnom bi, zbog
(u suprotnom bi, zbog 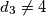 , slijedilo da
, slijedilo da 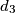 ima prost djelitelj veći od 2 pa
ima prost djelitelj veći od 2 pa 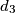 ne bi bio treći najmanji djelitelj od
ne bi bio treći najmanji djelitelj od  ). Sada imamo
). Sada imamo 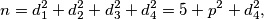 a budući da je
a budući da je  paran i
paran i  neparan, slijedi da
neparan, slijedi da 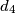 mora biti paran, tj.
mora biti paran, tj. 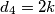 . Uočimo da
. Uočimo da  ima sve proste faktore veće ili jednake
ima sve proste faktore veće ili jednake  (u suprotnom
(u suprotnom  ne bi bio treći najmanji djelitelj od
ne bi bio treći najmanji djelitelj od  ). Pretpostavimo da
). Pretpostavimo da  ima prost djelitelj
ima prost djelitelj  koji je strogo veći od
koji je strogo veći od  (uočimo da
(uočimo da  mora biti neparan). Tada je
mora biti neparan). Tada je  djelitelj od
djelitelj od  koji je manji od
koji je manji od 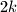 , pa bi četvrti najmanji djelitelj od
, pa bi četvrti najmanji djelitelj od  bio neparan. Kontradikcija, dakle,
bio neparan. Kontradikcija, dakle,  je jedini prost djelitelj od
je jedini prost djelitelj od  . Budući da je
. Budući da je 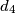 četvrti najmanji djelitelj od
četvrti najmanji djelitelj od  , slijedi
, slijedi 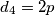 .
.Dakle, imamo
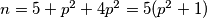 . Budući da
. Budući da  dijeli
dijeli  i
i  ne dijeli
ne dijeli 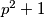 , vidimo da
, vidimo da  mora dijeliti
mora dijeliti  . Dakle,
. Dakle, 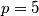 i
i 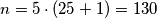 je jedini broj s traženim svojstvom.
je jedini broj s traženim svojstvom.  Školjka
Školjka 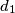 ,
, 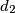 ,
,