Školjka Neocijenjeno
23. veljače 2016. 13:32 (8 godine, 9 mjeseci)
Sakrij rješenje
Sakrij rješenje
Za okruglim stolom sjedi 10 učenika. Svaki od učenika zamisli jedan realan broj i taj broj priopći samo svojim susjedima (učenicima koji sjede lijevo i desno od njega) tako da ga pritom drugi učenici ne čuju. Nakon toga, idući u krug, svaki učenik javno kaže aritmetičku sredinu dva broja koja je saznao od svojih susjeda. Ako su redom izrečeni brojevi 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, koji je broj zamislio učenik koji je javno rekao broj 6?
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Zbroj brojeva koje neki učenik sazna dvaput je veći od broja koji učenik javno izgovori. Zato je učenik koji je javno izgovorio broj 5 saznao brojeve čiji je zbroj jednak 10. Uočimo da su, prema uvjetu zadatka, njegovi susjedi javno rekli brojeve 4 i 6.
Dakle, ako je učenik koji je javno izgovorio broj 6 zamislio broj
, onda je učenik koji je javno izgovorio broj 4 zamislio broj 
.
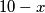Promatrajmo sada učenika koji je javno izgovorio broj 3. Taj je učenik saznao dva broja čiji je zbroj jednak 6, a jedan od tih brojeva jednak je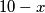 (od učenika koji je javno izgovorio broj 4). Zato je drugi broj, koji je saznao od učenika koji je javno izgovorio broj 2, jednak 
.
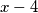Analogno, učenik koji je javno izgovorio broj 8 morao je zamisliti broj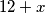
. No, učenik koji je javno izgovorio broj 7 saznao je dva broja čiji je zbroj jednak 14, pa imamo jednadžbu 
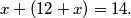Zato je 
, tj. učenik koji je javno izgovorio broj 6 zamislio je broj 1.
Dakle, ako je učenik koji je javno izgovorio broj 6 zamislio broj
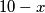, onda je učenik koji je javno izgovorio broj 4 zamislio broj .Promatrajmo sada učenika koji je javno izgovorio broj 3. Taj je učenik saznao dva broja čiji je zbroj jednak 6, a jedan od tih brojeva jednak je
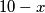(od učenika koji je javno izgovorio broj 4). Zato je drugi broj, koji je saznao od učenika koji je javno izgovorio broj 2, jednak 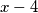.Analogno, učenik koji je javno izgovorio broj 8 morao je zamisliti broj
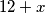. No, učenik koji je javno izgovorio broj 7 saznao je dva broja čiji je zbroj jednak 14, pa imamo jednadžbu 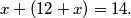Zato je , tj. učenik koji je javno izgovorio broj 6 zamislio je broj 1.