Neocijenjeno
23. veljače 2016. 13:32 (10 godine)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
(Link na skicu)
Označimo stranice trokuta standardno sa
standardno sa  te sa
te sa  njegov poluopseg. Neka je
njegov poluopseg. Neka je  središte upisane kružnice tog trokuta i neka su
središte upisane kružnice tog trokuta i neka su  ,
,  , tim redom, dirališta upisane kružnice i stranica
, tim redom, dirališta upisane kružnice i stranica  i
i  .
.
Budući da je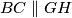 , trokuti
, trokuti  i
i 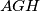 su slični (to su trokuti s jednakim kutovima), a potpuno analogno slijedi i da su trokuti
su slični (to su trokuti s jednakim kutovima), a potpuno analogno slijedi i da su trokuti 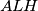 i
i 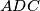 slični.
slični.
Budući da su odsječci tangenti iz neke točke na kružnicu međusobno jednake duljine, vrijedi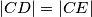 ,
, 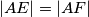 ,
, 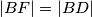 . Odavde dobivamo
. Odavde dobivamo 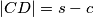 , a zbog prethodno dokazanih sličnosti slijedi
, a zbog prethodno dokazanih sličnosti slijedi 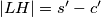 (gdje smo sa
(gdje smo sa 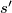 ,
, 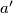 ,
, 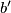 ,
, 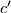 redom označili poluopseg i duljine stranica trokuta
redom označili poluopseg i duljine stranica trokuta 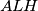 ).
).
No, budući da su točke i
i  dirališta tangenti na upisanu kružnicu iz točke
dirališta tangenti na upisanu kružnicu iz točke  , imamo
, imamo 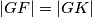 , a analogno dobivamo
, a analogno dobivamo 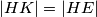 . Sada slijedi
. Sada slijedi 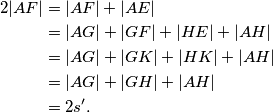 Dakle,
Dakle, 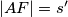 pa
pa 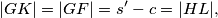 što je i trebalo pokazati.
što je i trebalo pokazati.
Označimo stranice trokuta
 standardno sa
standardno sa  te sa
te sa  njegov poluopseg. Neka je
njegov poluopseg. Neka je  središte upisane kružnice tog trokuta i neka su
središte upisane kružnice tog trokuta i neka su  ,
,  , tim redom, dirališta upisane kružnice i stranica
, tim redom, dirališta upisane kružnice i stranica  i
i  .
.Budući da je
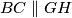 , trokuti
, trokuti  i
i 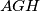 su slični (to su trokuti s jednakim kutovima), a potpuno analogno slijedi i da su trokuti
su slični (to su trokuti s jednakim kutovima), a potpuno analogno slijedi i da su trokuti 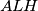 i
i 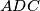 slični.
slični.Budući da su odsječci tangenti iz neke točke na kružnicu međusobno jednake duljine, vrijedi
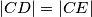 ,
, 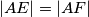 ,
, 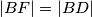 . Odavde dobivamo
. Odavde dobivamo 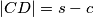 , a zbog prethodno dokazanih sličnosti slijedi
, a zbog prethodno dokazanih sličnosti slijedi 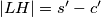 (gdje smo sa
(gdje smo sa 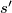 ,
, 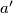 ,
, 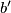 ,
, 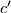 redom označili poluopseg i duljine stranica trokuta
redom označili poluopseg i duljine stranica trokuta 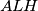 ).
).No, budući da su točke
 i
i  dirališta tangenti na upisanu kružnicu iz točke
dirališta tangenti na upisanu kružnicu iz točke  , imamo
, imamo 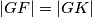 , a analogno dobivamo
, a analogno dobivamo 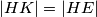 . Sada slijedi
. Sada slijedi 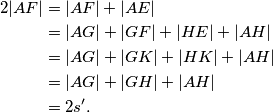 Dakle,
Dakle, 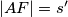 pa
pa 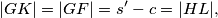 što je i trebalo pokazati.
što je i trebalo pokazati.  Školjka
Školjka  u točki
u točki  . Neka su točke
. Neka su točke  , tim redom, na stranicama
, tim redom, na stranicama  takve da su pravci
takve da su pravci 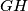 i
i  paralelni te da je pravac
paralelni te da je pravac  sjecište pravaca
sjecište pravaca  i
i 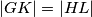 .
.