Neocijenjeno
26. veljače 2016. 13:40 (10 godine)
Korisnik: grga
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 3. (Sakrij tekst zadatka)
Zadatak: Simulacija županijskog 2016. za prvi razred zadatak 3. (Sakrij tekst zadatka)
Za okruglim stolom sjedi 10 učenika. Svaki od učenika zamisli jedan realan broj i taj broj priopći samo svojim susjedima (učenicima koji sjede lijevo i desno od njega) tako da ga pritom drugi učenici ne čuju. Nakon toga, idući u krug, svaki učenik javno kaže aritmetičku sredinu dva broja koja je saznao od svojih susjeda. Ako su redom izrečeni brojevi 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, koji je broj zamislio učenik koji je javno rekao broj 6?
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
evo jednog zapravo identicnog rjesenja, ali malo drukcije zapisanog, tako da se pokaze da se zapravo radi o sustavu jednadbi.
neka su ucenici zamislili redom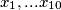 (onaj ucenik koji je izrekao
(onaj ucenik koji je izrekao  zamislio je
zamislio je  , ..., onaj koji je izrekao
, ..., onaj koji je izrekao  zamislio je
zamislio je 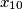 )
)
sad, ako pogledamo ucenika koji je izgovorio , znamo da vrijedi
, znamo da vrijedi 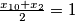 , tj
, tj 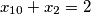 .
.
slicno ako pogledamo ucenika koji je izgovorio znamo
znamo 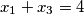 .
.
slicno, dolazimo do sustava s jednadbi i
jednadbi i  nepoznanica (broj u zagradi oznacava redni broj jednadbe, to ce nam trebati kasnije):
nepoznanica (broj u zagradi oznacava redni broj jednadbe, to ce nam trebati kasnije):
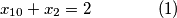
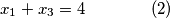
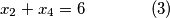
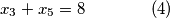
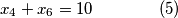
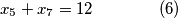
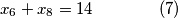
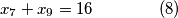
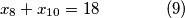
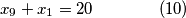
ovaj sustav, iako ima jednadbi i
jednadbi i  nepoznanica, se dosta lako rijesi. pogotovo jer su nepoznanice s parnim i neparnim indexima "odvojene", pa ga mozemo promatrati kao
nepoznanica, se dosta lako rijesi. pogotovo jer su nepoznanice s parnim i neparnim indexima "odvojene", pa ga mozemo promatrati kao  sustava
sustava 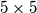 , a posto nas zadatak trazi samo
, a posto nas zadatak trazi samo 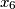 , dovoljno je gledati samo jedan sustav
, dovoljno je gledati samo jedan sustav 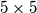 . u sluzbenom rjesenju je zapravo indirektno opisano rjesavanje ovog sustava, pogledajmo kako:
. u sluzbenom rjesenju je zapravo indirektno opisano rjesavanje ovog sustava, pogledajmo kako:
oznacimo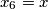 .
.
iz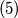 slijedi
slijedi 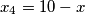 .
.
iz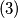 slijedi
slijedi 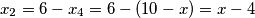 .
.
.. sad ide ovaj dio sa "analogno" iz sluzbenog..
iz slijedi
slijedi 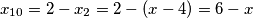 .
.
iz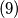 slijedi
slijedi 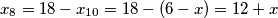 .
.
.. i sad za kraj imamo ..
iz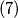 slijedi
slijedi 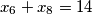 , odnosno
, odnosno 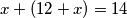 , pa ispada
, pa ispada 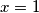 .
.
naravno, dani podsustav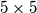 se mogao rijesiti raznim redosljedom supstitucija, ovo je bio samo jedan od mogucih.
se mogao rijesiti raznim redosljedom supstitucija, ovo je bio samo jedan od mogucih.
neka su ucenici zamislili redom
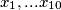 (onaj ucenik koji je izrekao
(onaj ucenik koji je izrekao  zamislio je
zamislio je  , ..., onaj koji je izrekao
, ..., onaj koji je izrekao  zamislio je
zamislio je 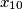 )
)sad, ako pogledamo ucenika koji je izgovorio
 , znamo da vrijedi
, znamo da vrijedi 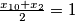 , tj
, tj 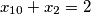 .
.slicno ako pogledamo ucenika koji je izgovorio
 znamo
znamo 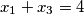 .
.slicno, dolazimo do sustava s
 jednadbi i
jednadbi i  nepoznanica (broj u zagradi oznacava redni broj jednadbe, to ce nam trebati kasnije):
nepoznanica (broj u zagradi oznacava redni broj jednadbe, to ce nam trebati kasnije):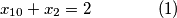
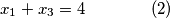
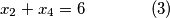
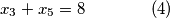
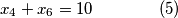
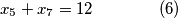
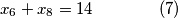
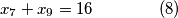
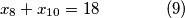
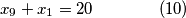
ovaj sustav, iako ima
 jednadbi i
jednadbi i  nepoznanica, se dosta lako rijesi. pogotovo jer su nepoznanice s parnim i neparnim indexima "odvojene", pa ga mozemo promatrati kao
nepoznanica, se dosta lako rijesi. pogotovo jer su nepoznanice s parnim i neparnim indexima "odvojene", pa ga mozemo promatrati kao  sustava
sustava 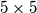 , a posto nas zadatak trazi samo
, a posto nas zadatak trazi samo 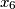 , dovoljno je gledati samo jedan sustav
, dovoljno je gledati samo jedan sustav 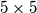 . u sluzbenom rjesenju je zapravo indirektno opisano rjesavanje ovog sustava, pogledajmo kako:
. u sluzbenom rjesenju je zapravo indirektno opisano rjesavanje ovog sustava, pogledajmo kako:oznacimo
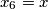 .
.iz
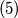 slijedi
slijedi 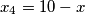 .
.iz
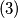 slijedi
slijedi 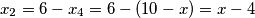 .
... sad ide ovaj dio sa "analogno" iz sluzbenog..
iz
 slijedi
slijedi 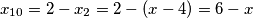 .
.iz
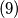 slijedi
slijedi 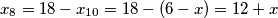 .
... i sad za kraj imamo ..
iz
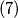 slijedi
slijedi 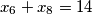 , odnosno
, odnosno 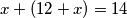 , pa ispada
, pa ispada 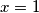 .
.naravno, dani podsustav
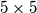 se mogao rijesiti raznim redosljedom supstitucija, ovo je bio samo jedan od mogucih.
se mogao rijesiti raznim redosljedom supstitucija, ovo je bio samo jedan od mogucih.  Školjka
Školjka