Točno
1. ožujka 2016. 20:02 (9 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ako je 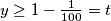 , gotovi smo. Pretpostavimo
, gotovi smo. Pretpostavimo 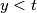 . Tada
. Tada 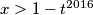 .
.
Dokazat ćemo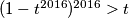 , iz čega slijedi tvrdnja zadatka jer
, iz čega slijedi tvrdnja zadatka jer 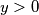 .
.
Vrijedi Bernoullijeva nejednakost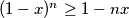 za
za 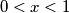 . Ona se zapravo lako dokaže AG-om:
. Ona se zapravo lako dokaže AG-om:
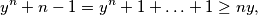
i uzmemo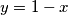 .
.
Primijenimo li je na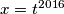 i
i 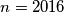 , dobivamo:
, dobivamo:
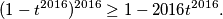
Ostaje dokazati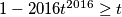 , što je ekvivalentno
, što je ekvivalentno 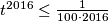 .
.
Poznato je da je:
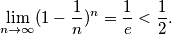
Lako se dobije da je funkcija pod limesom rastuća, tj. teži tom limesu odozdo. Zato:
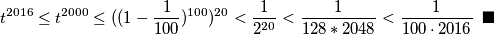
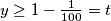 , gotovi smo. Pretpostavimo
, gotovi smo. Pretpostavimo 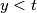 . Tada
. Tada 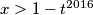 .
.Dokazat ćemo
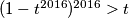 , iz čega slijedi tvrdnja zadatka jer
, iz čega slijedi tvrdnja zadatka jer 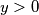 .
.Vrijedi Bernoullijeva nejednakost
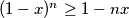 za
za 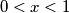 . Ona se zapravo lako dokaže AG-om:
. Ona se zapravo lako dokaže AG-om: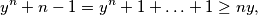
i uzmemo
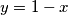 .
.Primijenimo li je na
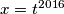 i
i 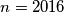 , dobivamo:
, dobivamo: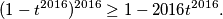
Ostaje dokazati
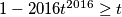 , što je ekvivalentno
, što je ekvivalentno 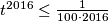 .
.Poznato je da je:
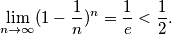
Lako se dobije da je funkcija pod limesom rastuća, tj. teži tom limesu odozdo. Zato:
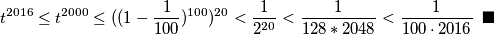
 Školjka
Školjka 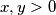 takvi da vrijedi
takvi da vrijedi 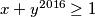 . Dokažite da vrijedi
. Dokažite da vrijedi 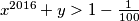 .
.