Točno
6. ožujka 2016. 14:25 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Za svako crno polje postoji centralnosimetrično koje je također crno (osim za centralno) pa bi trebao biti paran broj crnih polja. Neparan je, pa slijedi da je centralno polje crno.
S obzirom da je za svako crno polje i njegovo cntrsim polje također crno, ovdje možemo govoriti o odabiru parova.
Preostala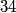 polja dijelimo u
polja dijelimo u  parova, a
parova, a 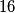 kojih treba obojati u
kojih treba obojati u  . Dakle, načina ima
. Dakle, načina ima 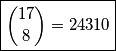 .
.
S obzirom da je za svako crno polje i njegovo cntrsim polje također crno, ovdje možemo govoriti o odabiru parova.
Preostala
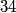 polja dijelimo u
polja dijelimo u  parova, a
parova, a 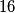 kojih treba obojati u
kojih treba obojati u  . Dakle, načina ima
. Dakle, načina ima 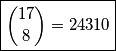 .
.  Školjka
Školjka 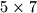 kojoj su sva polja bijela, potrebno je obojati točno
kojoj su sva polja bijela, potrebno je obojati točno 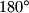 oko središta ploče. Na koliko je načina to moguće napraviti?
oko središta ploče. Na koliko je načina to moguće napraviti?