Točno
6. ožujka 2016. 19:34 (9 godine, 11 mjeseci)
Kvadratna ploča podijeljena je na 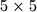 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
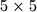 jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.
jediničnih kvadrata (polja). Na nju postavljamo osam triomina, tako da samo jedno polje ploče ostane nepokriveno.Triomino je lik sastavljen od tri jedinična kvadrata kao na slici:
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Odredi koja sve polja dane kvadratne ploče mogu ostati nepokrivena pri takvom popločavanju.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Obojimo ploču crno i bijelo kao na "slici":
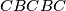
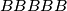
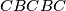
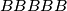
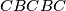
Imamo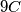 i
i 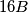 polja.
polja.
Imamo dva tipa triomina: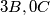 ili
ili 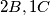 . Ako prvih ima
. Ako prvih ima  , tada drugih ima
, tada drugih ima  , a bijelih polja
, a bijelih polja 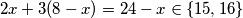 pa je jedino moguće
pa je jedino moguće 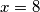 odnosno izbačeno polje je crne boje.
odnosno izbačeno polje je crne boje.
Preostaje dati primjere za sva tri tipa crnog polja na slici: kutno polje, centralno polje, polje na središtu brida. Nije potrebno zasebno davati primjere za sva crna polja jer su po simetriji ekvivalentna.
Evo popločavanja (izbačeno polje označeno s , iste pločice označene istim brojem).
, iste pločice označene istim brojem).
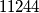
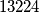
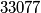
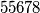
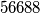 za centralno polje izbačeno
za centralno polje izbačeno
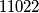
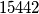
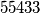
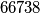
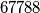 za sredinu brida
za sredinu brida
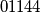
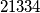
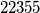
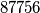
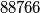 za kutno polje
za kutno polje
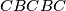
Imamo
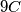 i
i 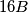 polja.
polja.Imamo dva tipa triomina:
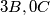 ili
ili 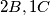 . Ako prvih ima
. Ako prvih ima  , tada drugih ima
, tada drugih ima  , a bijelih polja
, a bijelih polja 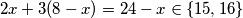 pa je jedino moguće
pa je jedino moguće 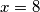 odnosno izbačeno polje je crne boje.
odnosno izbačeno polje je crne boje.Preostaje dati primjere za sva tri tipa crnog polja na slici: kutno polje, centralno polje, polje na središtu brida. Nije potrebno zasebno davati primjere za sva crna polja jer su po simetriji ekvivalentna.
Evo popločavanja (izbačeno polje označeno s
 , iste pločice označene istim brojem).
, iste pločice označene istim brojem).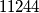
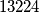
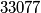
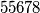
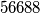 za centralno polje izbačeno
za centralno polje izbačeno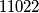
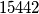
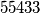
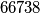
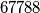 za sredinu brida
za sredinu brida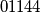
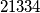
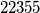
 za kutno polje
za kutno polje  Školjka
Školjka