Točno
6. ožujka 2016. 19:21 (9 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a) Rješenje ćemo dobiti tako da ćemo od ukupnog broja permutacija oduzeti nepovoljne odnosno one gdje su  i
i  susjedni.
susjedni.
Skup možemo u niz staviti na
možemo u niz staviti na  načina dok preostalih
načina dok preostalih  brojeva na
brojeva na  mjesta raspoređujemo na
mjesta raspoređujemo na 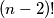 načina. Dakle imamo
načina. Dakle imamo 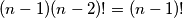 načina.
načina.
Analogno se radi sa skupom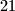 pa je sveukupno u igri
pa je sveukupno u igri 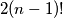 načina.
načina.
Rješenje je onda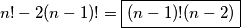 ,
,
b) Radi se po istom principu ali je nešto kompliciranije. Naći ćemo način da neka dva budu susjedna (tako svaka dva) i od toga oduzeti broj slučajeva kad je onaj treći prije njih (da nebi dvaput brojali isto)(prije, ne poslije, jer poslije spada pod isto to ali od druga dva broja, opet da nebi brojali previše).
Općenito za rasporediti broja kao susjede imamo kao što smo gore izračunali
broja kao susjede imamo kao što smo gore izračunali 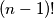 načina. Da bi tri bila susjedna analogno postoji
načina. Da bi tri bila susjedna analogno postoji 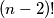 načina. Takvih varijanti od dva broja ima
načina. Takvih varijanti od dva broja ima  .
.
Rješenje je onda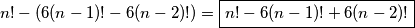 .
.
 i
i  susjedni.
susjedni.Skup
 možemo u niz staviti na
možemo u niz staviti na  načina dok preostalih
načina dok preostalih  brojeva na
brojeva na  mjesta raspoređujemo na
mjesta raspoređujemo na 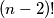 načina. Dakle imamo
načina. Dakle imamo 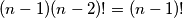 načina.
načina.Analogno se radi sa skupom
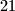 pa je sveukupno u igri
pa je sveukupno u igri 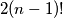 načina.
načina.Rješenje je onda
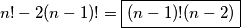 ,
,b) Radi se po istom principu ali je nešto kompliciranije. Naći ćemo način da neka dva budu susjedna (tako svaka dva) i od toga oduzeti broj slučajeva kad je onaj treći prije njih (da nebi dvaput brojali isto)(prije, ne poslije, jer poslije spada pod isto to ali od druga dva broja, opet da nebi brojali previše).
Općenito za rasporediti
 broja kao susjede imamo kao što smo gore izračunali
broja kao susjede imamo kao što smo gore izračunali 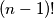 načina. Da bi tri bila susjedna analogno postoji
načina. Da bi tri bila susjedna analogno postoji 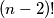 načina. Takvih varijanti od dva broja ima
načina. Takvih varijanti od dva broja ima  .
.Rješenje je onda
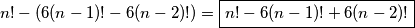 .
.  Školjka
Školjka  Koliko ima permutacija skupa
Koliko ima permutacija skupa 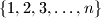 u kojima brojevi
u kojima brojevi  Koliko ima permutacija skupa
Koliko ima permutacija skupa 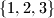 nisu susjedna?
nisu susjedna?