Točno
15. ožujka 2016. 23:45 (9 godine, 11 mjeseci)
Let
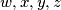
are non-negative reals such that
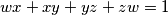
. Show that
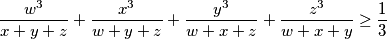
.
%V0
Let $w, x, y, z$ are non-negative reals such that $wx + xy + yz + zw = 1$. Show that
$$\frac {w^3}{x + y + z} + \frac {x^3}{w + y + z} + \frac {y^3}{w + x + z} + \frac {z^3}{w + x + y}\geq \frac {1}{3}$$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uocimo da uvijet mozemo zapisati kao
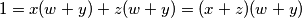
Prema Holderovoj nejednakosti vrijedi:
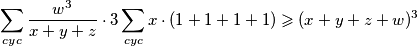
pa nakon djeljenja prethodnog izraza sa
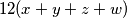
dobivamo
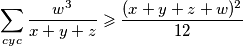
pa je dovoljno pokazati
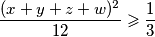
odnosno
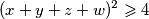
nakon korjenovanja, sto smijemo jer su
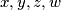
pozitivni dobivamo
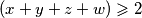
oznacimo sada
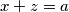
i
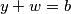
tada vrijedi
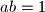
pa jednakost prelazi u
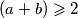
sto vrijedi po A-G nejdnakosti
%V0
Uocimo da uvijet mozemo zapisati kao $ 1=x(w+y)+z(w+y)=(x+z)(w+y) $
Prema Holderovoj nejednakosti vrijedi:
$ \displaystyle \sum\limits_{cyc}{ \frac{w^3}{x+y+z}} \cdot 3\sum\limits_{cyc}{x} \cdot (1+1+1+1) \geqslant (x+y+z+w)^3 $
pa nakon djeljenja prethodnog izraza sa $ 12(x+y+z+w) $ dobivamo
$ \displaystyle \sum\limits_{cyc}{ \frac{w^3}{x+y+z}} \geqslant \frac{(x+y+z+w)^2}{12} $
pa je dovoljno pokazati
$ \displaystyle \frac{(x+y+z+w)^2}{12} \geqslant \frac{1}{3} $
odnosno
$ \displaystyle (x+y+z+w)^2 \geqslant 4 $
nakon korjenovanja, sto smijemo jer su $ x,y,z,w $ pozitivni dobivamo
$ \displaystyle (x+y+z+w) \geqslant 2 $
oznacimo sada $ x+z=a $ i $ y+w=b $ tada vrijedi $ ab=1 $ pa jednakost prelazi u
$ \displaystyle (a+b) \geqslant 2 $ sto vrijedi po A-G nejdnakosti
| 1. travnja 2016. 17:16 | grga | Točno |