Točno
20. ožujka 2016. 19:06 (9 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Trivijalno je uvidjeti da su sljedeći četverokuti tetivni: 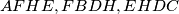 .
.
Iz toga slijedi: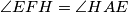 i
i 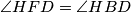 . Kako je
. Kako je 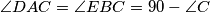 slijedi
slijedi 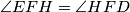 . Kako je i
. Kako je i 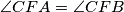 konačno slijedi i
konačno slijedi i 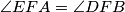 .
.
Zbog vršnih kuteva nadopunjujemo: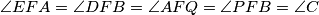 .
.
Neka je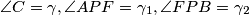 . Primijetimo
. Primijetimo 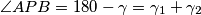 .
.
Po jednadžbama zbroja kutova u trokutu se dobiva:
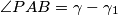
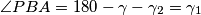
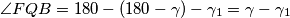 .
.
Kako je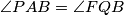 slijedi da je
slijedi da je 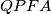 tetivan četverokut.
tetivan četverokut.
Sada je iz toga:
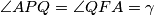 te je
te je
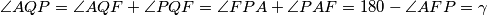 .
.
Iz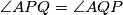 slijedi
slijedi 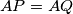 , što je i trebalo dokazati.
, što je i trebalo dokazati.
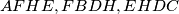 .
. Iz toga slijedi:
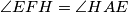 i
i 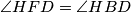 . Kako je
. Kako je 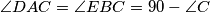 slijedi
slijedi 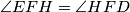 . Kako je i
. Kako je i 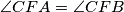 konačno slijedi i
konačno slijedi i 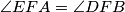 .
.Zbog vršnih kuteva nadopunjujemo:
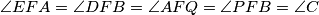 .
.Neka je
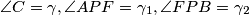 . Primijetimo
. Primijetimo 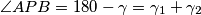 .
.Po jednadžbama zbroja kutova u trokutu se dobiva:
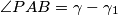
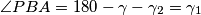
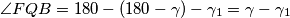 .
.Kako je
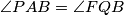 slijedi da je
slijedi da je 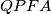 tetivan četverokut.
tetivan četverokut.Sada je iz toga:
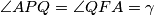 te je
te je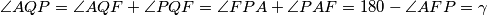 .
.Iz
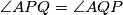 slijedi
slijedi 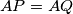 , što je i trebalo dokazati.
, što je i trebalo dokazati. Ocjene: (1)
Komentari:
grga, 4. svibnja 2016. 14:46
 Školjka
Školjka  be an acute triangle with
be an acute triangle with 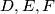 the feet of the altitudes lying on
the feet of the altitudes lying on 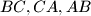 respectively. One of the intersection points of the line
respectively. One of the intersection points of the line  and the circumcircle is
and the circumcircle is 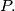 The lines
The lines 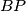 and
and 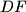 meet at point
meet at point 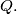 Prove that
Prove that 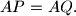
 ortocentar.
ortocentar.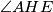 i
i 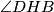 vrsni al i ovo je ok
vrsni al i ovo je ok