rhldj, 21. ožujka 2016. 20:20
%V0
Hvala, evo sredio sam.
ikicic, 21. ožujka 2016. 18:38
Preporučujem korištenje $$ ... $$ umjesto $ ... $ kako bi razlomci bili veći. Može i pomoću
\displaystyle:
$frac{a + b}{c}$ vs. $\displaystyle \frac{a + b}{c}$:
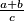
vs.
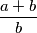
%V0
Preporučujem korištenje \$\$ ... \$\$ umjesto \$ ... \$ kako bi razlomci bili veći. Može i pomoću [i]\\displaystyle[/i]:
[i]\$\frac{a + b}{c}\$ vs. \$\\displaystyle \\frac{a + b}{c}\$[/i]:
$\frac{a + b}{c}$ vs. $\displaystyle \frac{a + b}{b}$