matsimic, 21. ožujka 2016. 21:35
Ili si ga mogao skratiti isključivo koristeći tvrdnju
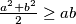
a ne verziju sa kvadratom zagrade.
%V0
Ili si ga mogao skratiti isključivo koristeći tvrdnju $\frac{a^2+b^2}{2} \geq ab$ a ne verziju sa kvadratom zagrade.
Zadnja promjena:
matsimic, 21. ožujka 2016. 21:35
rhldj, 21. ožujka 2016. 20:36
E sad kad bi još znao šta je to ... :)
Hvala, potražio sam, čini se zanimljivo
%V0
E sad kad bi još znao šta je to ... :)
Hvala, potražio sam, čini se zanimljivo
ikicic, 21. ožujka 2016. 18:34
Mislim da se korak s određivanjem maksimuma
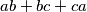
mogao skratiti korištenjem monotonog preuređenja vektora, iz kojeg odmah slijedi da je
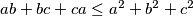
. Rješenje je inače sasvim ok.
%V0
Mislim da se korak s određivanjem maksimuma $ab + bc + ca$ mogao skratiti korištenjem monotonog preuređenja vektora, iz kojeg odmah slijedi da je $ab + bc + ca \leq a^2 + b^2 + c^2$. Rješenje je inače sasvim ok.