Neocijenjeno
21. ožujka 2016. 15:07 (9 godine, 11 mjeseci)
Dana je dvadeset i jedna točka kao na slici.
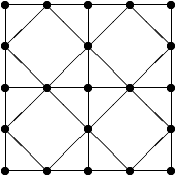
Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za .
.
Kažemo da je prirodni broj dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.
a) Dokaži da je broj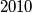 dohvatljiv.
dohvatljiv.
b) Dokaži da broj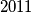 nije dohvatljiv.
nije dohvatljiv.

Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za
 .
.Kažemo da je prirodni broj
 dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.a) Dokaži da je broj
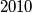 dohvatljiv.
dohvatljiv.b) Dokaži da broj
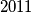 nije dohvatljiv.
nije dohvatljiv. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a){{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Ako povučemo 10 pravaca kao što je prikazano, povećali smo broj pridružen svakoj točki za dva, ponavljanjem postupka 1005 puta dobijemo 2010 u svakoj točki
b)Pretpostavimo suprotno tj, da je dohvatljiv. Gledajmo vrhove najveceg kvadrata, moguće je povećati broj pridružen uz njih samo pravcima kojima pripadaju stranice najvećeg kvadrata. Bez gubitka općenitosti prepostavimo da su brojevi na točkama s horizontalne strane parni, a s vertikalne neparni. Uzimajući u obzir ostale vrhove i stranice, brojevi na vertikalnim stranicama vanjskog kvadrata su neparni, a na horizontalnim parni. Moraju postojati pravci dijagonalni na te stranice jer imamo nepopunjene vrhove. U jednom potezu bi ucrtali pravac koji dira dvije točke na susjednim stranicama povećavajući im iznos za 1. Pri toj promijeni im mijenja parnost tako da je ukupan broj parnih točaka na vanjskim stranicama invarijantan tj. 6. Tu imamo kontradikciju jer svaka točka mora biti 2011, a taj broj je neparan što znači da parne točke ne postoje.
Ako povučemo 10 pravaca kao što je prikazano, povećali smo broj pridružen svakoj točki za dva, ponavljanjem postupka 1005 puta dobijemo 2010 u svakoj točki
b)Pretpostavimo suprotno tj, da je dohvatljiv. Gledajmo vrhove najveceg kvadrata, moguće je povećati broj pridružen uz njih samo pravcima kojima pripadaju stranice najvećeg kvadrata. Bez gubitka općenitosti prepostavimo da su brojevi na točkama s horizontalne strane parni, a s vertikalne neparni. Uzimajući u obzir ostale vrhove i stranice, brojevi na vertikalnim stranicama vanjskog kvadrata su neparni, a na horizontalnim parni. Moraju postojati pravci dijagonalni na te stranice jer imamo nepopunjene vrhove. U jednom potezu bi ucrtali pravac koji dira dvije točke na susjednim stranicama povećavajući im iznos za 1. Pri toj promijeni im mijenja parnost tako da je ukupan broj parnih točaka na vanjskim stranicama invarijantan tj. 6. Tu imamo kontradikciju jer svaka točka mora biti 2011, a taj broj je neparan što znači da parne točke ne postoje.
Komentari:
ikicic, 21. ožujka 2016. 18:30
Nisam siguran koliko je dobra ideja omoguciti stavljanje linkova na vanjske slike.
Jedan od razloga je to sto bi slika mogla postati nedostupna nakon X godina (a to zna biti jako iritantno).
Razmisljao jesam o tome kako bi se upload rjesenja trebao olaksati na nacin da korisnici mogu uploadati fotku rukom pisanog rjesenja (ili kao u ovom primjeru, skice).
Za sad mi se cini najjednostavnije napraviti da i rjesenja mogu imati attachmente pa da se tako uploadaju slike.
Ali mislim da nece skoro to biti napravljeno, jer je u planu prva neka tehnicka promjena koja ce oduzeti puno vremena.
Jedan od razloga je to sto bi slika mogla postati nedostupna nakon X godina (a to zna biti jako iritantno).
Razmisljao jesam o tome kako bi se upload rjesenja trebao olaksati na nacin da korisnici mogu uploadati fotku rukom pisanog rjesenja (ili kao u ovom primjeru, skice).
Za sad mi se cini najjednostavnije napraviti da i rjesenja mogu imati attachmente pa da se tako uploadaju slike.
Ali mislim da nece skoro to biti napravljeno, jer je u planu prva neka tehnicka promjena koja ce oduzeti puno vremena.
Zadnja promjena: ikicic, 21. ožujka 2016. 18:31
marin049, 21. ožujka 2016. 15:59
marin049, 21. ožujka 2016. 15:59
ikicic, 21. ožujka 2016. 15:20
 Školjka
Školjka