Točno
6. ožujka 2014. 17:23 (11 godine, 11 mjeseci)
Pokažite da za svaka dva pozitivna broja

i

vrijedi nejednakost
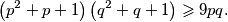
%V0
Pokažite da za svaka dva pozitivna broja $p$ i $q$ vrijedi nejednakost $$\left(p^2+p+1\right)\left(q^2+q+1\right) \geqslant 9pq \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Koristimo aritmetičko geometrijsku nejednakost za broje
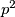
,

i

. Te sređivanjem dobijemo
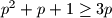
. Isti postupak uradimo i za brojeve
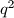
,

i

te dobijemo
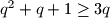
. Nakon toga pomonozimo te dvije nejednakosti gdje dobijemo
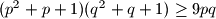
što je i trebalo dokazati.
%V0
Koristimo aritmetičko geometrijsku nejednakost za broje $p^2$ , $p$ i $1$. Te sređivanjem dobijemo $p^2+p+1 \ge 3p$. Isti postupak uradimo i za brojeve $q^2$, $q$ i $1$ te dobijemo $q^2+q+1 \ge 3q$. Nakon toga pomonozimo te dvije nejednakosti gdje dobijemo $(p^2+p+1)(q^2+q+1) \ge 9pq$ što je i trebalo dokazati.
| 22. studenoga 2012. 01:20 | ikicic | Točno |
| 23. studenoga 2012. 20:22 | mljulj | Točno |
| 27. studenoga 2012. 15:31 | kokan | Točno |