Zadatak mozemo zapisati kao
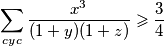
mnozenjem sa
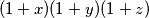
dobivamo ekvivalentnu nejednakost
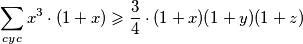
zapisivati cu
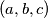
sto mi oznacava
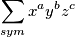
sada jednakost prelazi u
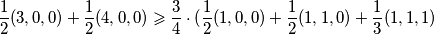
sada je nakon mnozenja sa

dovoljno pokazati
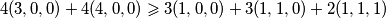
korištenjem
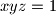
dobivamo sljedece nejednakosti koje vrijede po Muirheadu
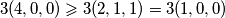
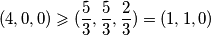
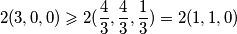
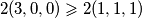
Zbrajanjem slijedi nejednakost koju smo htjeli pokazati
%V0
Zadatak mozemo zapisati kao
$ \displaystyle \sum\limits_{cyc}{ \frac{x^3}{(1+y)(1+z)}} \geqslant \frac{3}{4} $
mnozenjem sa $ \displaystyle (1+x)(1+y)(1+z) $ dobivamo ekvivalentnu nejednakost
$ \displaystyle \sum\limits_{cyc}{x^3 \cdot (1+x)} \geqslant \frac{3}{4} \cdot (1+x)(1+y)(1+z) $
zapisivati cu $ \displaystyle (a,b,c) $ sto mi oznacava $ \displaystyle \sum\limits_{sym}{ x^a y^b z^c} $
sada jednakost prelazi u
$ \displaystyle \frac{1}{2} (3,0,0) + \frac{1}{2} (4,0,0) \geqslant \frac{3}{4} \cdot ( \frac{1}{2} (1,0,0)+ \frac{1}{2} (1,1,0)+ \frac{1}{3} (1,1,1) $
sada je nakon mnozenja sa $ 8 $ dovoljno pokazati
$ \displaystyle 4 (3,0,0) + 4 (4,0,0) \geqslant 3 (1,0,0)+ 3 (1,1,0)+2 (1,1,1) $
korištenjem $ xyz=1 $ dobivamo sljedece nejednakosti koje vrijede po Muirheadu
$ \displaystyle 3 (4,0,0) \geqslant 3 (2,1,1)=3(1,0,0) $
$ \displaystyle (4,0,0) \geqslant ( \frac{5}{3} , \frac{5}{3} , \frac{2}{3} )=(1,1,0) $
$ \displaystyle 2(3,0,0) \geqslant 2 ( \frac{4}{3} , \frac{4}{3} , \frac{1}{3} )=2(1,1,0) $
$ \displaystyle 2(3,0,0) \geqslant 2 (1,1,1) $
Zbrajanjem slijedi nejednakost koju smo htjeli pokazati