Točno
23. ožujka 2016. 00:16 (9 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
buduci da je jednakost homogena mozemo pretpostaviti 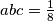 , sada koristeci uvjet pocetnu nejednakost zapisemo ovako
, sada koristeci uvjet pocetnu nejednakost zapisemo ovako
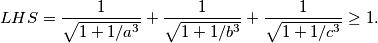
lako se dokaze da opcenito vrijedi
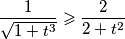 za svaki
za svaki 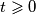 sada koristimo
sada koristimo 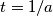 ,
, 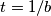 ,
, 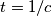 pa imamo
pa imamo
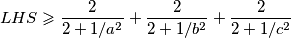
pa zelimo pokazati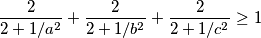
uvedimo supstituciju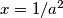 ,
, 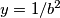 ,
, 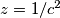 tada nas uvjet prelazi u
tada nas uvjet prelazi u 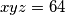
mnozenjem prethdone nejednakosti s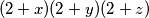 dobivamo ekvivalentnu nejednakost
dobivamo ekvivalentnu nejednakost
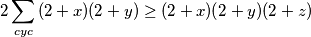
odnosno uz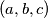 sto mi oznacava
sto mi oznacava 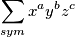
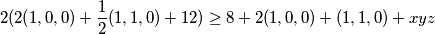 odnosno
odnosno
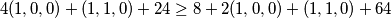 pa treba pokazati
pa treba pokazati
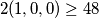
sada imamo zbog A-G nejednakosti![\displaystyle 2(1,0,0)=4(x+y+z) \geq 4 \cdot 3 \cdot \sqrt[3]{xyz}=48](/media/m/0/2/a/02a56efd2794b5cba9d129f5707f4a41.png) sto je trebalo i pokazati
sto je trebalo i pokazati
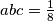 , sada koristeci uvjet pocetnu nejednakost zapisemo ovako
, sada koristeci uvjet pocetnu nejednakost zapisemo ovako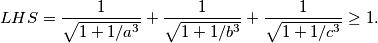
lako se dokaze da opcenito vrijedi
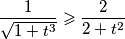 za svaki
za svaki 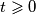 sada koristimo
sada koristimo 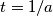 ,
, 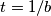 ,
, 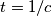 pa imamo
pa imamo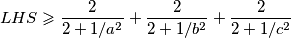
pa zelimo pokazati
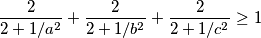
uvedimo supstituciju
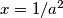 ,
, 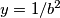 ,
, 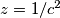 tada nas uvjet prelazi u
tada nas uvjet prelazi u 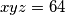
mnozenjem prethdone nejednakosti s
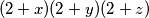 dobivamo ekvivalentnu nejednakost
dobivamo ekvivalentnu nejednakost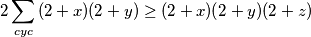
odnosno uz
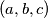 sto mi oznacava
sto mi oznacava 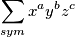
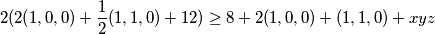 odnosno
odnosno 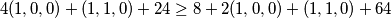 pa treba pokazati
pa treba pokazati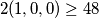
sada imamo zbog A-G nejednakosti
![\displaystyle 2(1,0,0)=4(x+y+z) \geq 4 \cdot 3 \cdot \sqrt[3]{xyz}=48](/media/m/0/2/a/02a56efd2794b5cba9d129f5707f4a41.png) sto je trebalo i pokazati
sto je trebalo i pokazati  Školjka
Školjka  ,
,