Točno
24. ožujka 2016. 23:58 (9 godine, 11 mjeseci)
Korisnik: IvanSincic
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Nazovimo dvije kružnice  i
i  "povezane" ako se dodiruju ili ako barem jedna od njih (WLOG
"povezane" ako se dodiruju ili ako barem jedna od njih (WLOG  ) dodiruje neku treću kružnicu koja je "povezana" s
) dodiruje neku treću kružnicu koja je "povezana" s  . Skup kružnica u kojem su one sve međusobno "povezane" nazovimo "grupica". Potrebno je dokazati da je sve kružnice u svakoj "grupici" moguće obojati u 4 boje kako zadatak traži.
. Skup kružnica u kojem su one sve međusobno "povezane" nazovimo "grupica". Potrebno je dokazati da je sve kružnice u svakoj "grupici" moguće obojati u 4 boje kako zadatak traži.
Dokažimo sljedeću tvrdnju:
U svakoj "grupici" postoji barem jedna kružnica koja dodiruje najviše 3 druge kružnice (u toj istoj "grupici")
Dokaz:
Pretpostavimo suprotno, postoji "grupica" u kojoj svaka kružnica dodiruje barem 4 druge kružnice (iste "grupice"). Promatrajmo jednu takvu "grupicu" i smjestimo ju u koordinatni sustav. Obratimo sada pažnju na kružnicu čije središte ima najmanju y koordinatu (ako ih ima više bilo koju od njih) i povucimo pravac paralelan s osi x kroz središte te kružnice ( ). Tu kružnicu dodiruju bar 4 druge kružnice čija ću središta označiti
). Tu kružnicu dodiruju bar 4 druge kružnice čija ću središta označiti 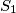 ,
, 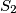 ,
, 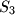 i
i 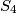 redom u smjeru kazaljke na satu oko
redom u smjeru kazaljke na satu oko  tako da je veličina kuta
tako da je veličina kuta 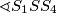 najveća (od kuteva
najveća (od kuteva 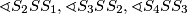 te
te 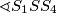 ). Primijetimo da vrijedi
). Primijetimo da vrijedi 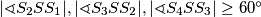 (zbog toga što sve kružnice imaju jednak radijus i nikoje dvije se ne sijeku) pa je minimalna vrijednost veličine kuta
(zbog toga što sve kružnice imaju jednak radijus i nikoje dvije se ne sijeku) pa je minimalna vrijednost veličine kuta 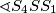 180°. Kako sve četiri kružnice moraju imati veću ili jednaku y koordinatu od kružnice oko
180°. Kako sve četiri kružnice moraju imati veću ili jednaku y koordinatu od kružnice oko  , zaključujemo da se to može dogoditi jedino za slučaj jednakosti, odnosno za
, zaključujemo da se to može dogoditi jedino za slučaj jednakosti, odnosno za 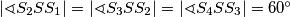 . No sada sa svake strane kružnice oko
. No sada sa svake strane kružnice oko  imamo još dvije kružnice čija središta imaju jednaku y koordinatu i za njih vrijedi ista stvar pa će i oko njih postojati kružnice čija središta imaju jednaku y koordinatu i to će se nastaviti u beskonačnost, ali kako "grupica" nema beskonačan broj kružnica unutar sebe, to je kontradikcija te zaključujemo da u svakoj "grupici" uvijek postoji barem jedna kružnica koja dodiruje najviše 3 druge.
imamo još dvije kružnice čija središta imaju jednaku y koordinatu i za njih vrijedi ista stvar pa će i oko njih postojati kružnice čija središta imaju jednaku y koordinatu i to će se nastaviti u beskonačnost, ali kako "grupica" nema beskonačan broj kružnica unutar sebe, to je kontradikcija te zaključujemo da u svakoj "grupici" uvijek postoji barem jedna kružnica koja dodiruje najviše 3 druge.
Promatrajmo sada neku "grupicu". Dokazali smo da postoji kružnica (WLOG ) koja dodiruje najviše tri druge kružnice unutar te grupice pa zbog toga boja kojom ćemo obojati
) koja dodiruje najviše tri druge kružnice unutar te grupice pa zbog toga boja kojom ćemo obojati  ovisi samo o bojama tih kružnica, a kako bojimo u četiri boje, uvijek će postojati boja kojom možemo obojati
ovisi samo o bojama tih kružnica, a kako bojimo u četiri boje, uvijek će postojati boja kojom možemo obojati  tako da su uvjeti zadatka zadovoljeni (možemo ju "dobro" obojati). Zbog te činjenice kružnicu
tako da su uvjeti zadatka zadovoljeni (možemo ju "dobro" obojati). Zbog te činjenice kružnicu  možemo obojati zadnju i dovoljno je dokazati da možemo "dobro" obojati ostale kružnice u "grupici". Broj kružnica koje sada moramo "dobro" obojati smanjio se za jedan i opet imamo "grupicu" u kojoj opet postoji barem jedna kružnica koja dodiruje najviše tri druge kružnice i postupak ponavljamo; smanjujemo broj kružnica dok ne dođemo do četiri kružnice koje obojimo u 4 različite boje. Sada redom unatrag bojimo kružnice koje smo ignorirali i ovime smo obojali sve kružnice u nekoj "grupici" u 4 boje čime je ovaj zadatak gotov.
možemo obojati zadnju i dovoljno je dokazati da možemo "dobro" obojati ostale kružnice u "grupici". Broj kružnica koje sada moramo "dobro" obojati smanjio se za jedan i opet imamo "grupicu" u kojoj opet postoji barem jedna kružnica koja dodiruje najviše tri druge kružnice i postupak ponavljamo; smanjujemo broj kružnica dok ne dođemo do četiri kružnice koje obojimo u 4 različite boje. Sada redom unatrag bojimo kružnice koje smo ignorirali i ovime smo obojali sve kružnice u nekoj "grupici" u 4 boje čime je ovaj zadatak gotov.
 i
i  "povezane" ako se dodiruju ili ako barem jedna od njih (WLOG
"povezane" ako se dodiruju ili ako barem jedna od njih (WLOG  ) dodiruje neku treću kružnicu koja je "povezana" s
) dodiruje neku treću kružnicu koja je "povezana" s  . Skup kružnica u kojem su one sve međusobno "povezane" nazovimo "grupica". Potrebno je dokazati da je sve kružnice u svakoj "grupici" moguće obojati u 4 boje kako zadatak traži.
. Skup kružnica u kojem su one sve međusobno "povezane" nazovimo "grupica". Potrebno je dokazati da je sve kružnice u svakoj "grupici" moguće obojati u 4 boje kako zadatak traži. Dokažimo sljedeću tvrdnju:
U svakoj "grupici" postoji barem jedna kružnica koja dodiruje najviše 3 druge kružnice (u toj istoj "grupici")
Dokaz:
Pretpostavimo suprotno, postoji "grupica" u kojoj svaka kružnica dodiruje barem 4 druge kružnice (iste "grupice"). Promatrajmo jednu takvu "grupicu" i smjestimo ju u koordinatni sustav. Obratimo sada pažnju na kružnicu čije središte ima najmanju y koordinatu (ako ih ima više bilo koju od njih) i povucimo pravac paralelan s osi x kroz središte te kružnice (
 ). Tu kružnicu dodiruju bar 4 druge kružnice čija ću središta označiti
). Tu kružnicu dodiruju bar 4 druge kružnice čija ću središta označiti 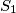 ,
, 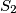 ,
, 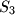 i
i 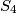 redom u smjeru kazaljke na satu oko
redom u smjeru kazaljke na satu oko  tako da je veličina kuta
tako da je veličina kuta 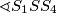 najveća (od kuteva
najveća (od kuteva 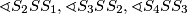 te
te 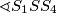 ). Primijetimo da vrijedi
). Primijetimo da vrijedi 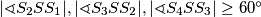 (zbog toga što sve kružnice imaju jednak radijus i nikoje dvije se ne sijeku) pa je minimalna vrijednost veličine kuta
(zbog toga što sve kružnice imaju jednak radijus i nikoje dvije se ne sijeku) pa je minimalna vrijednost veličine kuta 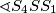 180°. Kako sve četiri kružnice moraju imati veću ili jednaku y koordinatu od kružnice oko
180°. Kako sve četiri kružnice moraju imati veću ili jednaku y koordinatu od kružnice oko  , zaključujemo da se to može dogoditi jedino za slučaj jednakosti, odnosno za
, zaključujemo da se to može dogoditi jedino za slučaj jednakosti, odnosno za 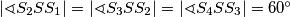 . No sada sa svake strane kružnice oko
. No sada sa svake strane kružnice oko  imamo još dvije kružnice čija središta imaju jednaku y koordinatu i za njih vrijedi ista stvar pa će i oko njih postojati kružnice čija središta imaju jednaku y koordinatu i to će se nastaviti u beskonačnost, ali kako "grupica" nema beskonačan broj kružnica unutar sebe, to je kontradikcija te zaključujemo da u svakoj "grupici" uvijek postoji barem jedna kružnica koja dodiruje najviše 3 druge.
imamo još dvije kružnice čija središta imaju jednaku y koordinatu i za njih vrijedi ista stvar pa će i oko njih postojati kružnice čija središta imaju jednaku y koordinatu i to će se nastaviti u beskonačnost, ali kako "grupica" nema beskonačan broj kružnica unutar sebe, to je kontradikcija te zaključujemo da u svakoj "grupici" uvijek postoji barem jedna kružnica koja dodiruje najviše 3 druge.Promatrajmo sada neku "grupicu". Dokazali smo da postoji kružnica (WLOG
 ) koja dodiruje najviše tri druge kružnice unutar te grupice pa zbog toga boja kojom ćemo obojati
) koja dodiruje najviše tri druge kružnice unutar te grupice pa zbog toga boja kojom ćemo obojati  ovisi samo o bojama tih kružnica, a kako bojimo u četiri boje, uvijek će postojati boja kojom možemo obojati
ovisi samo o bojama tih kružnica, a kako bojimo u četiri boje, uvijek će postojati boja kojom možemo obojati  tako da su uvjeti zadatka zadovoljeni (možemo ju "dobro" obojati). Zbog te činjenice kružnicu
tako da su uvjeti zadatka zadovoljeni (možemo ju "dobro" obojati). Zbog te činjenice kružnicu  možemo obojati zadnju i dovoljno je dokazati da možemo "dobro" obojati ostale kružnice u "grupici". Broj kružnica koje sada moramo "dobro" obojati smanjio se za jedan i opet imamo "grupicu" u kojoj opet postoji barem jedna kružnica koja dodiruje najviše tri druge kružnice i postupak ponavljamo; smanjujemo broj kružnica dok ne dođemo do četiri kružnice koje obojimo u 4 različite boje. Sada redom unatrag bojimo kružnice koje smo ignorirali i ovime smo obojali sve kružnice u nekoj "grupici" u 4 boje čime je ovaj zadatak gotov.
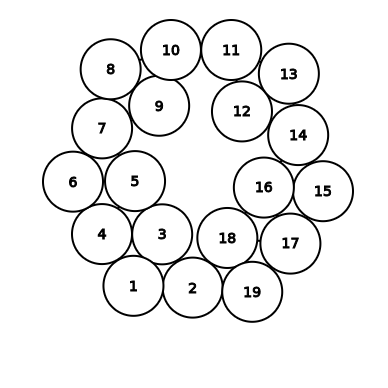
možemo obojati zadnju i dovoljno je dokazati da možemo "dobro" obojati ostale kružnice u "grupici". Broj kružnica koje sada moramo "dobro" obojati smanjio se za jedan i opet imamo "grupicu" u kojoj opet postoji barem jedna kružnica koja dodiruje najviše tri druge kružnice i postupak ponavljamo; smanjujemo broj kružnica dok ne dođemo do četiri kružnice koje obojimo u 4 različite boje. Sada redom unatrag bojimo kružnice koje smo ignorirali i ovime smo obojali sve kružnice u nekoj "grupici" u 4 boje čime je ovaj zadatak gotov.  Školjka
Školjka  kružnica radijusa
kružnica radijusa  tako da se nijedne dvije ne sijeku (kružnice se mogu dodirivati). Dokažite da je kružnice moguće obojati u
tako da se nijedne dvije ne sijeku (kružnice se mogu dodirivati). Dokažite da je kružnice moguće obojati u  boje tako da se nijedan par kružnica iste boje ne dodiruje.
boje tako da se nijedan par kružnica iste boje ne dodiruje.