Točno
24. ožujka 2016. 13:45 (9 godine, 11 mjeseci)
Korisnik: IvanSincic
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 2. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 2. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Uvjet je ekvivalentan s 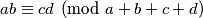
Očito vrijedi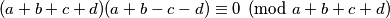 pa imamo:
pa imamo:
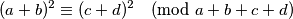
Odnosno:
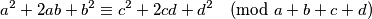
Sada zbog uvjeta zadatka imamo:
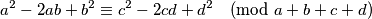
Te nakon faktorizacije:
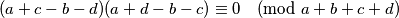
Dalje nastavljamo kontradikcijom. Neka je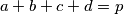 gdje je
gdje je  prost broj.
prost broj.
Očito jedan od brojeva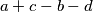 i
i 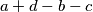 mora biti kongruentan
mora biti kongruentan 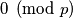 te iz toga dobivamo
te iz toga dobivamo 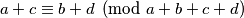 odnosno
odnosno 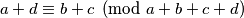 . Kako su
. Kako su 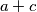 i
i 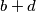 odnosno
odnosno 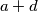 i
i 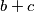 prirodni brojevi manji od
prirodni brojevi manji od  , oni su jednaki (
, oni su jednaki (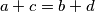 ili
ili 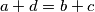 ) i
) i  je jednak zbroju dva jednaka prirodna broja pa je samim time
je jednak zbroju dva jednaka prirodna broja pa je samim time  paran broj, ali kako je sigurno veći od 2 i po pretpostavci prost, dobivamo kontradikciju te
paran broj, ali kako je sigurno veći od 2 i po pretpostavci prost, dobivamo kontradikciju te 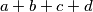 ne može biti prost.
ne može biti prost.
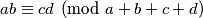
Očito vrijedi
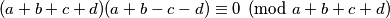 pa imamo:
pa imamo: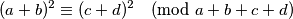
Odnosno:
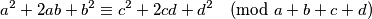
Sada zbog uvjeta zadatka imamo:
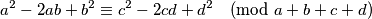
Te nakon faktorizacije:
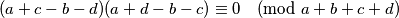
Dalje nastavljamo kontradikcijom. Neka je
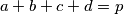 gdje je
gdje je  prost broj.
prost broj.Očito jedan od brojeva
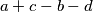 i
i 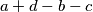 mora biti kongruentan
mora biti kongruentan 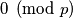 te iz toga dobivamo
te iz toga dobivamo 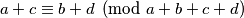 odnosno
odnosno 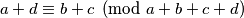 . Kako su
. Kako su 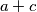 i
i 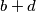 odnosno
odnosno 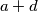 i
i 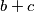 prirodni brojevi manji od
prirodni brojevi manji od  , oni su jednaki (
, oni su jednaki (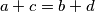 ili
ili 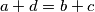 ) i
) i  je jednak zbroju dva jednaka prirodna broja pa je samim time
je jednak zbroju dva jednaka prirodna broja pa je samim time  paran broj, ali kako je sigurno veći od 2 i po pretpostavci prost, dobivamo kontradikciju te
paran broj, ali kako je sigurno veći od 2 i po pretpostavci prost, dobivamo kontradikciju te 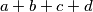 ne može biti prost.
ne može biti prost. Ocjene: (2)
Komentari:
IvanSincic, 24. ožujka 2016. 13:37
Ako misliš na to da je jedan od ova dva člana na kraju jednak nula, imaš pravo, nisam pogledao taj slučaj. Inače originalno rješenje mi je išlo da uz pretpostavku da je 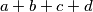 prost pokažem da mora biti paran, a kako je sigurno veći od 2 to je kontradikcija, ali kada sam došao do tog dijela rješenja činilo mi se zgodnije koristiti činjenicu da su brojevi
prost pokažem da mora biti paran, a kako je sigurno veći od 2 to je kontradikcija, ali kada sam došao do tog dijela rješenja činilo mi se zgodnije koristiti činjenicu da su brojevi 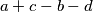 i
i 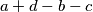 manji od
manji od 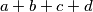 po apsolutnoj vrijednosti i zaboravio sam na slučaj ako su jednaki 0.
po apsolutnoj vrijednosti i zaboravio sam na slučaj ako su jednaki 0.
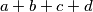 prost pokažem da mora biti paran, a kako je sigurno veći od 2 to je kontradikcija, ali kada sam došao do tog dijela rješenja činilo mi se zgodnije koristiti činjenicu da su brojevi
prost pokažem da mora biti paran, a kako je sigurno veći od 2 to je kontradikcija, ali kada sam došao do tog dijela rješenja činilo mi se zgodnije koristiti činjenicu da su brojevi 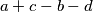 i
i 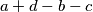 manji od
manji od 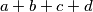 po apsolutnoj vrijednosti i zaboravio sam na slučaj ako su jednaki 0.
po apsolutnoj vrijednosti i zaboravio sam na slučaj ako su jednaki 0. dpaleka, 23. ožujka 2016. 23:17
 Školjka
Školjka  ,
,  ,
,  ,
,  prirodni brojevi takvi da je
prirodni brojevi takvi da je 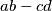 djeljiv s
djeljiv s 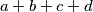 . Dokažite da je broj
. Dokažite da je broj 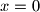 ?
? 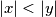 ,
,  ne može dijeliti
ne može dijeliti  .
.