Točno
23. ožujka 2016. 23:32 (9 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
nakon kvadriranja ove zagrade imamo
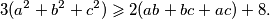
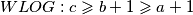 odnosno to mozemo zapisati ovako
odnosno to mozemo zapisati ovako  pa dalje
pa dalje 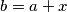 to jest
to jest 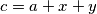 za neke
za neke 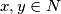
sada nakon sto ovo uvrstimo dobivamo
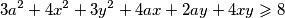
to mozemo zapisati malo ljepse
 ......
...... 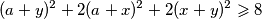 sada zbog
sada zbog 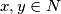 imamo
imamo 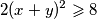
buduci da su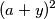 i
i 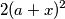 kvadrati nekih cijelih brojeva vrijedi
kvadrati nekih cijelih brojeva vrijedi
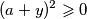 i
i 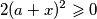 pa vrijedi
pa vrijedi  pokazimo jos slucaj jednakosti
pokazimo jos slucaj jednakosti 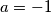 i
i 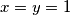 odnosno
odnosno
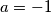 odnosno
odnosno 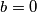 i
i 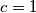 lako se vidi da se tada zaista postiže jednakost
lako se vidi da se tada zaista postiže jednakost
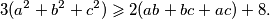
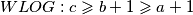 odnosno to mozemo zapisati ovako
odnosno to mozemo zapisati ovako  pa dalje
pa dalje 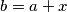 to jest
to jest 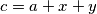 za neke
za neke 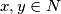
sada nakon sto ovo uvrstimo dobivamo
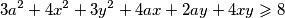
to mozemo zapisati malo ljepse
 ......
...... 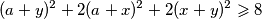 sada zbog
sada zbog 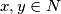 imamo
imamo 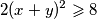
buduci da su
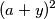 i
i 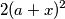 kvadrati nekih cijelih brojeva vrijedi
kvadrati nekih cijelih brojeva vrijedi 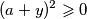 i
i 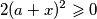 pa vrijedi
pa vrijedi  pokazimo jos slucaj jednakosti
pokazimo jos slucaj jednakosti 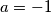 i
i 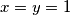 odnosno
odnosno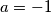 odnosno
odnosno 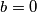 i
i 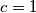 lako se vidi da se tada zaista postiže jednakost
lako se vidi da se tada zaista postiže jednakost  Školjka
Školjka  različiti cijeli brojevi. Dokažite da vrijedi:
različiti cijeli brojevi. Dokažite da vrijedi: