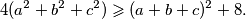Točno
24. ožujka 2016. 19:16 (9 godine, 11 mjeseci)
Korisnik: PETARMAT
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Nakon kvadriranja i sređivanja slijedi ova nejednakost:
3 a^2 + 3 b^2 + 3 c^2 >= 2 ab + 2 bc + 2 ca + 8 <=> (a-b)^2 + (b-c)^2 + (c-a)^2 + a^2 + b^2 + c^2 >= 8
Dalje u rješenju ću koristiti nepoznanice x,y,z kao neku permutaciju od brojeva a,b,c.
Kako su a,b,c različiti cijeli brojevi, slijedi da je |a - b| >= 1, |b - c| >= 1, |c - a| >= 1. Pretpostavimo da kod sve tri nejednakosti vrijedi jednakost.
Imamo 2 slučaja:
a) a je parno => b neparno => c parno => a neparno =><=
b) a je neparno => b parno => c neparno => a parno =><=
Znači da se kod barem jedne nejednakosti ne postiže jednakost, tj. vrijedi |x-y| >= 2. Iz toga slijedi da je: (a-b)^2 + (b-c)^2 + (c-a)^2 >= 1^2 + 1^2 + 2^2 = 6. (1)
Kako su a,b,c cijeli brojevi, slijedi da je |a| >= 0, |b| >= 0, |c| >= 0. Pretpostavimo da barem dvije od tri nejednakosti vrijedi nejednakost.
Tada bi vrijedilo: |x| = 0 = |y| => x = 0 = y =><=
Znači da se kod barem dvije nejednakosti ne postiže jednakost, tj. vrijedi |x| >= 1 i |y| >= 1. Iz toga slijedi da je: a^2 + b^2 + c^2 >= 1 + 1 + 0 = 2. (2)
(1) + (2) => (a-b)^2 + (b-c)^2 + (c-a)^2 + a^2 + b^2 + c^2 >= 8
Q.E.D.
3 a^2 + 3 b^2 + 3 c^2 >= 2 ab + 2 bc + 2 ca + 8 <=> (a-b)^2 + (b-c)^2 + (c-a)^2 + a^2 + b^2 + c^2 >= 8
Dalje u rješenju ću koristiti nepoznanice x,y,z kao neku permutaciju od brojeva a,b,c.
Kako su a,b,c različiti cijeli brojevi, slijedi da je |a - b| >= 1, |b - c| >= 1, |c - a| >= 1. Pretpostavimo da kod sve tri nejednakosti vrijedi jednakost.
Imamo 2 slučaja:
a) a je parno => b neparno => c parno => a neparno =><=
b) a je neparno => b parno => c neparno => a parno =><=
Znači da se kod barem jedne nejednakosti ne postiže jednakost, tj. vrijedi |x-y| >= 2. Iz toga slijedi da je: (a-b)^2 + (b-c)^2 + (c-a)^2 >= 1^2 + 1^2 + 2^2 = 6. (1)
Kako su a,b,c cijeli brojevi, slijedi da je |a| >= 0, |b| >= 0, |c| >= 0. Pretpostavimo da barem dvije od tri nejednakosti vrijedi nejednakost.
Tada bi vrijedilo: |x| = 0 = |y| => x = 0 = y =><=
Znači da se kod barem dvije nejednakosti ne postiže jednakost, tj. vrijedi |x| >= 1 i |y| >= 1. Iz toga slijedi da je: a^2 + b^2 + c^2 >= 1 + 1 + 0 = 2. (2)
(1) + (2) => (a-b)^2 + (b-c)^2 + (c-a)^2 + a^2 + b^2 + c^2 >= 8
Q.E.D.
 Školjka
Školjka  različiti cijeli brojevi. Dokažite da vrijedi:
različiti cijeli brojevi. Dokažite da vrijedi: