ikicic, 24. ožujka 2016. 20:52
Aha, sve ok, ja sam nešto zabrijao. Zamislio sam
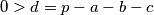
umjesto
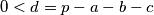
xD
%V0
Aha, sve ok, ja sam nešto zabrijao. Zamislio sam $0 > d = p - a - b - c$ umjesto $0 < d = p - a - b - c$ xD
PETARMAT, 24. ožujka 2016. 20:39
a, b, c i d su prirodni brojevi, pa je b,d > 0, a onda je a + c < a + b + c + d = p. Analogno i za b + c < p.
Možeš li detaljnije pojasniti kako si došao do
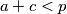
i
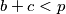
?
%V0
a, b, c i d su prirodni brojevi, pa je b,d > 0, a onda je a + c < a + b + c + d = p. Analogno i za b + c < p.
[quote]Možeš li detaljnije pojasniti kako si došao do $a + c < p$ i $b + c < p$?[/quote]
Zadnja promjena:
PETARMAT, 24. ožujka 2016. 20:40
ikicic, 24. ožujka 2016. 19:26
Možeš li detaljnije pojasniti kako si došao do
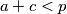
i
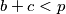
?
%V0
Možeš li detaljnije pojasniti kako si došao do $a + c < p$ i $b + c < p$?
 Školjka
Školjka  ,
,  ,
,  ,
,  prirodni brojevi takvi da je
prirodni brojevi takvi da je 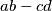 djeljiv s
djeljiv s 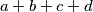 . Dokažite da je broj
. Dokažite da je broj 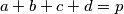 , gdje je
, gdje je  neki prost broj.
neki prost broj.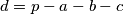 .
.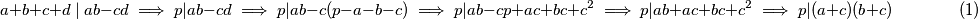
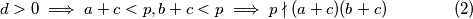
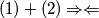
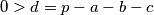 umjesto
umjesto 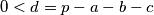 xD
xD 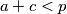 i
i 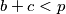 ?
?