Točno
25. ožujka 2016. 12:59 (9 godine, 11 mjeseci)
Korisnik: PETARMAT
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Spojimo u parove ovih  točaka te provucimo kroz njih
točaka te provucimo kroz njih 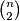 pravaca. Obzirom da je to konačno mnogo pravaca, slijedi da možemo odabrati neki pravac
pravaca. Obzirom da je to konačno mnogo pravaca, slijedi da možemo odabrati neki pravac  tako da nije paralelan s niti jednim od ovih
tako da nije paralelan s niti jednim od ovih 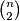 pravaca.
pravaca.
Označimo kružnice na neki način s brojevima od do
do  . Neka je
. Neka je 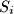 središte kružnice
središte kružnice 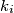 koju smo označili s
koju smo označili s  za
za 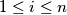 . Na početku su sve kružnice obojane u boju
. Na početku su sve kružnice obojane u boju  (ona nije konačna boja), a možemo ih obojati u jednu od boja iz skupa
(ona nije konačna boja), a možemo ih obojati u jednu od boja iz skupa 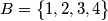 .
.
Dokazat ćemo tvrdnju zadatka tako što ćemo pronaći konstrukciju bojanja.
Konstrukcija
Na početku postavimo pravac negdje u ravninu tako da ne sijeće niti jednu kružnicu te da su sve kružnice s jedne strane pravca
negdje u ravninu tako da ne sijeće niti jednu kružnicu te da su sve kružnice s jedne strane pravca  . Pomičemo pravac
. Pomičemo pravac  u smjeru kružnica sve dok sve kružnice ne prijeđu s jedne strane pravca na drugu. Kako je pravac
u smjeru kružnica sve dok sve kružnice ne prijeđu s jedne strane pravca na drugu. Kako je pravac  neparalelan s svim ostalim pravcima, slijedi da u jednom trenutku može najviše jedna kružnica prijeći s jedne strane pravca
neparalelan s svim ostalim pravcima, slijedi da u jednom trenutku može najviše jedna kružnica prijeći s jedne strane pravca  na drugu. Promotrimo u nekom trenutku kružnicu
na drugu. Promotrimo u nekom trenutku kružnicu 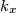 koja prelazi na drugu stranu pravca (pod "prelaskom" podrazumijevamo prelazak središta
koja prelazi na drugu stranu pravca (pod "prelaskom" podrazumijevamo prelazak središta 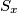 na drugu stranu pravca
na drugu stranu pravca  ). Nju ćemo obojati u boju (čiji je broj najmanji mogući) iz skupa
). Nju ćemo obojati u boju (čiji je broj najmanji mogući) iz skupa  tako da se taj broj boje ne poklapa sa brojevima boja kružnica koje
tako da se taj broj boje ne poklapa sa brojevima boja kružnica koje 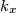 dodiruje. To uvijek možemo zbog Lemme jer se ne može dogoditi da neka kružnica ima boju
dodiruje. To uvijek možemo zbog Lemme jer se ne može dogoditi da neka kružnica ima boju  , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  .
.
Na početku obojamo kružnicu koja je najbliža pravcu u boju
u boju  , te dalje provodimo već objašnjeni postupak bojanja za ostalih
, te dalje provodimo već objašnjeni postupak bojanja za ostalih 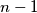 kružnica. Q.E.D.
kružnica. Q.E.D.
Dokaz Lemme
Tvrdnja: Ne može se dogoditi da neka kružnica ima boju , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  .
.
Pretpostavimo suprotno, tj. da neka kružnica ima boju , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  . Provest ćemo dokaz ako se radi o
. Provest ćemo dokaz ako se radi o  kružnice koje imaju boju veću od
kružnice koje imaju boju veću od  , jer je dokaz analogan i za
, jer je dokaz analogan i za  i za
i za  (kružnica ne može imati više od
(kružnica ne može imati više od  susjeda).
susjeda).
Neka kružnica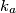 ima boju
ima boju  , a kružnice
, a kružnice 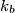 ,
, 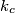 ,
, 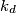 i
i 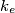 (koje je dodiruju) boju veću od
(koje je dodiruju) boju veću od  (neka vrijedi da su kružnice
(neka vrijedi da su kružnice 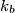 ,
, 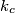 ,
, 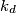 i
i 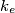 poredane u smjeru kazalje na satu oko kružnice
poredane u smjeru kazalje na satu oko kružnice 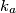 ).
).
Vrijedi:
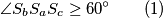
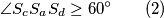
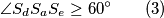
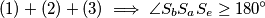
Kako je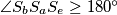 , slijedi da je nemoguće da su u nekom trenutku središta
, slijedi da je nemoguće da su u nekom trenutku središta 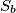 i
i 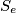 već "prešla" pravac
već "prešla" pravac  , a da
, a da 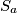 još nije. Kontradikcija.
još nije. Kontradikcija.
 točaka te provucimo kroz njih
točaka te provucimo kroz njih 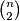 pravaca. Obzirom da je to konačno mnogo pravaca, slijedi da možemo odabrati neki pravac
pravaca. Obzirom da je to konačno mnogo pravaca, slijedi da možemo odabrati neki pravac  tako da nije paralelan s niti jednim od ovih
tako da nije paralelan s niti jednim od ovih 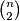 pravaca.
pravaca.Označimo kružnice na neki način s brojevima od
 do
do  . Neka je
. Neka je 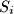 središte kružnice
središte kružnice 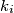 koju smo označili s
koju smo označili s  za
za 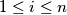 . Na početku su sve kružnice obojane u boju
. Na početku su sve kružnice obojane u boju  (ona nije konačna boja), a možemo ih obojati u jednu od boja iz skupa
(ona nije konačna boja), a možemo ih obojati u jednu od boja iz skupa 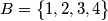 .
.Dokazat ćemo tvrdnju zadatka tako što ćemo pronaći konstrukciju bojanja.
Konstrukcija
Na početku postavimo pravac
 negdje u ravninu tako da ne sijeće niti jednu kružnicu te da su sve kružnice s jedne strane pravca
negdje u ravninu tako da ne sijeće niti jednu kružnicu te da su sve kružnice s jedne strane pravca  . Pomičemo pravac
. Pomičemo pravac  u smjeru kružnica sve dok sve kružnice ne prijeđu s jedne strane pravca na drugu. Kako je pravac
u smjeru kružnica sve dok sve kružnice ne prijeđu s jedne strane pravca na drugu. Kako je pravac  neparalelan s svim ostalim pravcima, slijedi da u jednom trenutku može najviše jedna kružnica prijeći s jedne strane pravca
neparalelan s svim ostalim pravcima, slijedi da u jednom trenutku može najviše jedna kružnica prijeći s jedne strane pravca  na drugu. Promotrimo u nekom trenutku kružnicu
na drugu. Promotrimo u nekom trenutku kružnicu 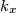 koja prelazi na drugu stranu pravca (pod "prelaskom" podrazumijevamo prelazak središta
koja prelazi na drugu stranu pravca (pod "prelaskom" podrazumijevamo prelazak središta 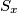 na drugu stranu pravca
na drugu stranu pravca  ). Nju ćemo obojati u boju (čiji je broj najmanji mogući) iz skupa
). Nju ćemo obojati u boju (čiji je broj najmanji mogući) iz skupa  tako da se taj broj boje ne poklapa sa brojevima boja kružnica koje
tako da se taj broj boje ne poklapa sa brojevima boja kružnica koje 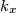 dodiruje. To uvijek možemo zbog Lemme jer se ne može dogoditi da neka kružnica ima boju
dodiruje. To uvijek možemo zbog Lemme jer se ne može dogoditi da neka kružnica ima boju  , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  .
.Na početku obojamo kružnicu koja je najbliža pravcu
 u boju
u boju  , te dalje provodimo već objašnjeni postupak bojanja za ostalih
, te dalje provodimo već objašnjeni postupak bojanja za ostalih 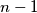 kružnica. Q.E.D.
kružnica. Q.E.D. Dokaz Lemme
Tvrdnja: Ne može se dogoditi da neka kružnica ima boju
 , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  .
.Pretpostavimo suprotno, tj. da neka kružnica ima boju
 , a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od
, a više od tri kružnice (koje dodiruju tu kružnicu) imaju boju veću od  . Provest ćemo dokaz ako se radi o
. Provest ćemo dokaz ako se radi o  kružnice koje imaju boju veću od
kružnice koje imaju boju veću od  , jer je dokaz analogan i za
, jer je dokaz analogan i za  i za
i za  (kružnica ne može imati više od
(kružnica ne može imati više od  susjeda).
susjeda).Neka kružnica
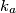 ima boju
ima boju  , a kružnice
, a kružnice 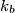 ,
, 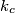 ,
, 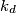 i
i 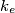 (koje je dodiruju) boju veću od
(koje je dodiruju) boju veću od  (neka vrijedi da su kružnice
(neka vrijedi da su kružnice 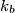 ,
, 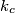 ,
, 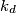 i
i 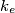 poredane u smjeru kazalje na satu oko kružnice
poredane u smjeru kazalje na satu oko kružnice 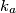 ).
).Vrijedi:
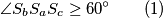
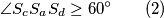
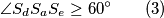
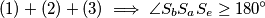
Kako je
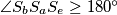 , slijedi da je nemoguće da su u nekom trenutku središta
, slijedi da je nemoguće da su u nekom trenutku središta 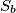 i
i 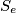 već "prešla" pravac
već "prešla" pravac  , a da
, a da 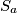 još nije. Kontradikcija.
još nije. Kontradikcija.  Školjka
Školjka