Točno
25. ožujka 2016. 17:05 (9 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da možemo.
Ako obojamo ploču kao šahovsku kvadrat prekriva crna i
crna i  bijela bolja,
bijela bolja,
a svaki bi tetromino prekrivao:
 crna i
crna i  bijelo ili
bijelo ili  bijela i
bijela i  crno polje.
crno polje.
+---+
| █ |
+---+---+
| □ | █ |
+---+---+
| █ |
+---+
ili
+---+
| □ |
+---+---+
| █ | □ |
+---+---+
| □ |
+---+
tj. svaki tetromino ima crno i
crno i  bijelo polje
bijelo polje 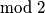 jer
jer 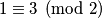 .
.
Na ploči imamo tetrominoa.
tetrominoa.
To znači da imamo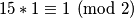 crnih i bijelih polja prekrivenih tetrominoima
crnih i bijelih polja prekrivenih tetrominoima
Kvadrat zauzima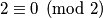 crnih i bijelih polja
crnih i bijelih polja
tj. ukupno imamo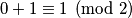 polja bilo koje boje.
polja bilo koje boje.
Ploča ima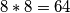 polja, tj.
polja, tj. 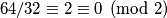 bilo koje boje
bilo koje boje
slijedi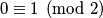 tj. imamo kontradikciju i zaključujemo da ne možemo popločati ploču.
tj. imamo kontradikciju i zaključujemo da ne možemo popločati ploču.
Ako obojamo ploču kao šahovsku kvadrat prekriva
 crna i
crna i  bijela bolja,
bijela bolja,a svaki bi tetromino prekrivao:
 crna i
crna i  bijelo ili
bijelo ili  bijela i
bijela i  crno polje.
crno polje.+---+
| █ |
+---+---+
| □ | █ |
+---+---+
| █ |
+---+
ili
+---+
| □ |
+---+---+
| █ | □ |
+---+---+
| □ |
+---+
tj. svaki tetromino ima
 crno i
crno i  bijelo polje
bijelo polje 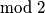 jer
jer 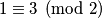 .
.Na ploči imamo
 tetrominoa.
tetrominoa.To znači da imamo
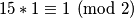 crnih i bijelih polja prekrivenih tetrominoima
crnih i bijelih polja prekrivenih tetrominoimaKvadrat zauzima
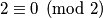 crnih i bijelih polja
crnih i bijelih poljatj. ukupno imamo
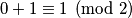 polja bilo koje boje.
polja bilo koje boje.Ploča ima
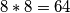 polja, tj.
polja, tj. 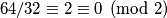 bilo koje boje
bilo koje bojeslijedi
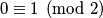 tj. imamo kontradikciju i zaključujemo da ne možemo popločati ploču.
tj. imamo kontradikciju i zaključujemo da ne možemo popločati ploču.  Školjka
Školjka 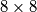 ploču jednim
ploču jednim 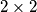 kvadratom i
kvadratom i