Točno
25. ožujka 2016. 18:07 (9 godine, 11 mjeseci)
Korisnik: Daniel_Sirola
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 4. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 4. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
skica
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Smjestimo taj pravokutnik u koordinatni sustav.
Neka je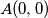 ,
, 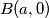 ,
, 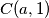 i
i 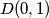 .
.
Lako nalazimo polovišta dužina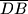 ,
,  i
i 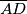 .
.
To su, redom,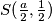 ,
, 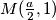 i
i 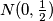 .
.
Sada možemo izračunati koeficijent smjera pravca .
.
To je prema formuli: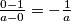
S obzirom da je simetrala neke dužine okomita na nju, ako je koeficijent smjera pravca na kojem leži ta dužina, onda je
koeficijent smjera pravca na kojem leži ta dužina, onda je 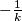 koeficijent smjera simetrale. (Tu tvrdnju smatram dovoljno poznatom, i ne namjeravam ju dokazivati)
koeficijent smjera simetrale. (Tu tvrdnju smatram dovoljno poznatom, i ne namjeravam ju dokazivati)
Dakle, neka je ta simetrala neki pravac .
.
Znamo da mu je koeficijent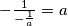 .
.
Također znamo da prolazi točkom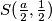 , te možemo izračunati njegov odsječak na
, te možemo izračunati njegov odsječak na  -osi.
-osi.
Neka je taj odsječak jednak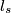 .
.
Znamo da vrijedi:
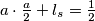
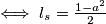 .
.
Sada znamo jednadžbu pravca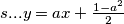
Sljedeći je korak izračunavanje koordinata točaka i
i  ..
..
Znamo da točka se nalazi na pravcima
se nalazi na pravcima  i
i  .
.
Tako možemo izračunati :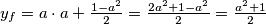
Odnosno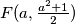 .
.
Točka se nalazi na pravcu
se nalazi na pravcu  i pravcu
i pravcu  .
.
Treba izračunati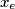 .
.
Vrijedi: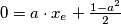
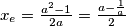
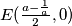 .
.
Sada po prijašnjoj formuli izračunavamo koeficijente smjera pravaca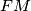 i
i 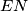 :
:
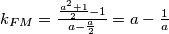
Analogno:
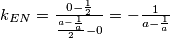
Sada lako primjećujemo :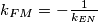
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
Smjestimo taj pravokutnik u koordinatni sustav.
Neka je
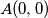 ,
, 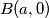 ,
, 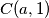 i
i 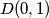 .
.Lako nalazimo polovišta dužina
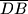 ,
,  i
i 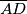 .
.To su, redom,
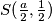 ,
, 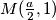 i
i 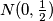 .
.Sada možemo izračunati koeficijent smjera pravca
 .
. To je prema formuli:
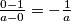
S obzirom da je simetrala neke dužine okomita na nju, ako je
 koeficijent smjera pravca na kojem leži ta dužina, onda je
koeficijent smjera pravca na kojem leži ta dužina, onda je 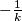 koeficijent smjera simetrale. (Tu tvrdnju smatram dovoljno poznatom, i ne namjeravam ju dokazivati)
koeficijent smjera simetrale. (Tu tvrdnju smatram dovoljno poznatom, i ne namjeravam ju dokazivati)Dakle, neka je ta simetrala neki pravac
 .
.Znamo da mu je koeficijent
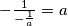 .
.Također znamo da prolazi točkom
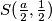 , te možemo izračunati njegov odsječak na
, te možemo izračunati njegov odsječak na  -osi.
-osi.Neka je taj odsječak jednak
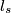 .
.Znamo da vrijedi:
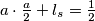
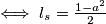 .
.Sada znamo jednadžbu pravca
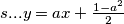
Sljedeći je korak izračunavanje koordinata točaka
 i
i  ..
..Znamo da točka
 se nalazi na pravcima
se nalazi na pravcima  i
i  .
.Tako možemo izračunati :
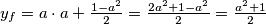
Odnosno
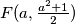 .
.Točka
 se nalazi na pravcu
se nalazi na pravcu 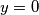 i pravcu
i pravcu  .
.Treba izračunati
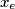 .
.Vrijedi:
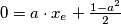
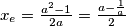
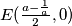 .
.Sada po prijašnjoj formuli izračunavamo koeficijente smjera pravaca
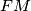 i
i 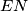 :
: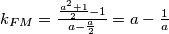
Analogno:
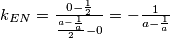
Sada lako primjećujemo :
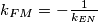
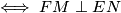
Ocjene: (2)
Komentari:
Daniel_Sirola, 25. ožujka 2016. 19:59
Zadnja promjena: Daniel_Sirola, 25. ožujka 2016. 19:59
Daniel_Sirola, 25. ožujka 2016. 19:52
ikicic, 25. ožujka 2016. 18:22
Daniel_Sirola, 25. ožujka 2016. 18:09
 Školjka
Školjka  . Simetrala dužine
. Simetrala dužine  siječe pravce
siječe pravce  i
i  redom u točkama
redom u točkama  i
i  polovišta dužina
polovišta dužina