Točno
25. ožujka 2016. 17:25 (9 godine, 11 mjeseci)
Korisnik: dpaleka
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 5. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ekvivalentan zadatak: U ravnini je dano  točaka tako da su svake dvije udaljene barem za
točaka tako da su svake dvije udaljene barem za  . Dokažite da je točke moguće obojati u 4 boje tako da nijedan par točaka iste boje nije udaljen točno za
. Dokažite da je točke moguće obojati u 4 boje tako da nijedan par točaka iste boje nije udaljen točno za  .
.
Neka se dvije točke dodiruju ako su udaljene točno za .
.
Vršimo indukciju po . Baza je trivijalna.
. Baza je trivijalna.
Promatrajmo konveksnu ljusku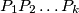 zadanog skupa točaka.
zadanog skupa točaka.
Ako je ona pravac, tvrdnja je trivijalna, inače postoji takav da je
takav da je 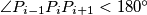 .
.
Kao u ostalim rješenjima, zbrajanjem kuteva lako se dobije da se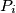 dodiruje s najviše
dodiruje s najviše  točke.
točke.
Po pretpostavci indukcije, možemo valjano obojati sve točke osim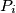 zanemarivši boju
zanemarivši boju 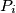 . Pošto se
. Pošto se 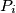 dodiruje s najviše
dodiruje s najviše  točke, postoji boja u koju je možemo obojati,
točke, postoji boja u koju je možemo obojati, 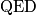 .
.
 točaka tako da su svake dvije udaljene barem za
točaka tako da su svake dvije udaljene barem za  . Dokažite da je točke moguće obojati u 4 boje tako da nijedan par točaka iste boje nije udaljen točno za
. Dokažite da je točke moguće obojati u 4 boje tako da nijedan par točaka iste boje nije udaljen točno za  .
.Neka se dvije točke dodiruju ako su udaljene točno za
 .
.Vršimo indukciju po
 . Baza je trivijalna.
. Baza je trivijalna.Promatrajmo konveksnu ljusku
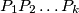 zadanog skupa točaka.
zadanog skupa točaka. Ako je ona pravac, tvrdnja je trivijalna, inače postoji
 takav da je
takav da je 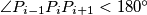 .
. Kao u ostalim rješenjima, zbrajanjem kuteva lako se dobije da se
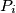 dodiruje s najviše
dodiruje s najviše  točke.
točke.Po pretpostavci indukcije, možemo valjano obojati sve točke osim
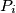 zanemarivši boju
zanemarivši boju 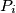 . Pošto se
. Pošto se 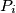 dodiruje s najviše
dodiruje s najviše  točke, postoji boja u koju je možemo obojati,
točke, postoji boja u koju je možemo obojati, 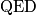 .
.  Školjka
Školjka  boje tako da se nijedan par kružnica iste boje ne dodiruje.
boje tako da se nijedan par kružnica iste boje ne dodiruje.