Točno
6. listopada 2016. 16:54 (9 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su 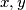 ,
, 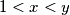 najmanji pozitivni djelitelji broja
najmanji pozitivni djelitelji broja  .
.
Tada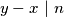 , ali taj broj je manji od
, ali taj broj je manji od  pa može biti samo
pa može biti samo 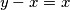 ili
ili 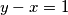 .
.
U prvom slučaju:
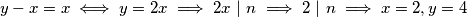
Neka je najmanji neparan broj različit od
najmanji neparan broj različit od  takav da
takav da 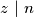 Očito
Očito 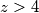 (jer su najmanji djelitelji poznati) ali tada i
(jer su najmanji djelitelji poznati) ali tada i 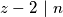 , a on je također neparan broj, što je u suprotnosti sa pretpostavkom da je
, a on je također neparan broj, što je u suprotnosti sa pretpostavkom da je  minimalan, pa zaključujemo da
minimalan, pa zaključujemo da  nema najmanjeg tj. nema niti jednog neparnog djelitelja većeg od
nema najmanjeg tj. nema niti jednog neparnog djelitelja većeg od  tj.
tj.  je potencija broja
je potencija broja  .
.
Očito za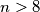 vrijedi
vrijedi 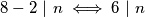 ali to je nemoguće, pa
ali to je nemoguće, pa 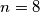 u ovom slučaju.
u ovom slučaju.
U drugom slučaju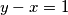 povlači da je jedan od njih paran pa opet
povlači da je jedan od njih paran pa opet 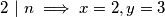 .
.
Očito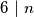 , pa je provjerom jedno rješenje
, pa je provjerom jedno rješenje 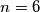 . Nadalje ako
. Nadalje ako 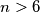 vrijedi i
vrijedi i 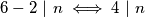 pa vrijedi i
pa vrijedi i 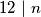 . Također dobivamo još jedno rješenje
. Također dobivamo još jedno rješenje 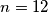 .
.
Nadalje, ako vrijedi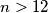 vrijedi (analogno gornjem postupku)
vrijedi (analogno gornjem postupku) 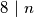 pa znamo da vrijedi i
pa znamo da vrijedi i 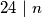 .
. 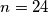 nije rješenje pa
nije rješenje pa 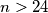 .
.
Nadalje, označimo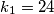 . Neka je
. Neka je  najveći neparni prosti faktor
najveći neparni prosti faktor  i neka funkcija
i neka funkcija  nije definirana na potencijama broja
nije definirana na potencijama broja  . Za neki
. Za neki 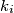 promatrajmo
promatrajmo 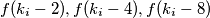 . Dvije od tih vrijednosti su za
. Dvije od tih vrijednosti su za 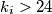 svakako definirane. Neka je
svakako definirane. Neka je 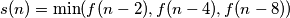 . Nadalje, neka je
. Nadalje, neka je 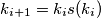 Po uvjetu zadatka, za svaki
Po uvjetu zadatka, za svaki 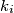 možemo zaključiti da
možemo zaključiti da 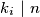 te možemo zaključiti da on nije najveći djelitelj
te možemo zaključiti da on nije najveći djelitelj  (jer sigurno postoji veći umnožak
(jer sigurno postoji veći umnožak 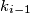 sa brojem iz skupa koji taj uvjet zadovoljava) što nam dozvoljava nastavak zaključivanja. Također, počimanje sa
sa brojem iz skupa koji taj uvjet zadovoljava) što nam dozvoljava nastavak zaključivanja. Također, počimanje sa 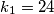 garantira
garantira 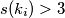 što nam svaki put garantira novog prostog djelitelja. Budući da možemo zaključiti da proizvoljno velik broj dijeli
što nam svaki put garantira novog prostog djelitelja. Budući da možemo zaključiti da proizvoljno velik broj dijeli  ,
,  u ovom slučaju ne postoji.
u ovom slučaju ne postoji.
Rješenja su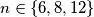 .
.
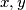 ,
, 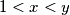 najmanji pozitivni djelitelji broja
najmanji pozitivni djelitelji broja  .
. Tada
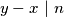 , ali taj broj je manji od
, ali taj broj je manji od  pa može biti samo
pa može biti samo 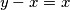 ili
ili 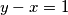 .
.U prvom slučaju:
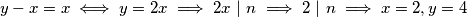
Neka je
 najmanji neparan broj različit od
najmanji neparan broj različit od  takav da
takav da 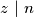 Očito
Očito 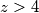 (jer su najmanji djelitelji poznati) ali tada i
(jer su najmanji djelitelji poznati) ali tada i 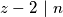 , a on je također neparan broj, što je u suprotnosti sa pretpostavkom da je
, a on je također neparan broj, što je u suprotnosti sa pretpostavkom da je  minimalan, pa zaključujemo da
minimalan, pa zaključujemo da  nema najmanjeg tj. nema niti jednog neparnog djelitelja većeg od
nema najmanjeg tj. nema niti jednog neparnog djelitelja većeg od  tj.
tj.  je potencija broja
je potencija broja  .
. Očito za
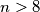 vrijedi
vrijedi 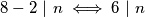 ali to je nemoguće, pa
ali to je nemoguće, pa 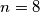 u ovom slučaju.
u ovom slučaju.U drugom slučaju
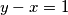 povlači da je jedan od njih paran pa opet
povlači da je jedan od njih paran pa opet 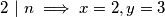 .
.Očito
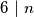 , pa je provjerom jedno rješenje
, pa je provjerom jedno rješenje 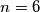 . Nadalje ako
. Nadalje ako 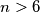 vrijedi i
vrijedi i 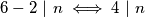 pa vrijedi i
pa vrijedi i 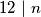 . Također dobivamo još jedno rješenje
. Također dobivamo još jedno rješenje 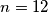 .
.Nadalje, ako vrijedi
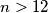 vrijedi (analogno gornjem postupku)
vrijedi (analogno gornjem postupku) 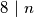 pa znamo da vrijedi i
pa znamo da vrijedi i 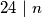 .
. 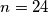 nije rješenje pa
nije rješenje pa 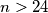 .
. Nadalje, označimo
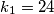 . Neka je
. Neka je  najveći neparni prosti faktor
najveći neparni prosti faktor  i neka funkcija
i neka funkcija  nije definirana na potencijama broja
nije definirana na potencijama broja  . Za neki
. Za neki 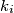 promatrajmo
promatrajmo 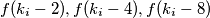 . Dvije od tih vrijednosti su za
. Dvije od tih vrijednosti su za 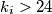 svakako definirane. Neka je
svakako definirane. Neka je 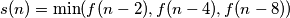 . Nadalje, neka je
. Nadalje, neka je 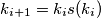 Po uvjetu zadatka, za svaki
Po uvjetu zadatka, za svaki 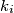 možemo zaključiti da
možemo zaključiti da 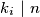 te možemo zaključiti da on nije najveći djelitelj
te možemo zaključiti da on nije najveći djelitelj  (jer sigurno postoji veći umnožak
(jer sigurno postoji veći umnožak 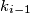 sa brojem iz skupa koji taj uvjet zadovoljava) što nam dozvoljava nastavak zaključivanja. Također, počimanje sa
sa brojem iz skupa koji taj uvjet zadovoljava) što nam dozvoljava nastavak zaključivanja. Također, počimanje sa 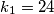 garantira
garantira 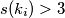 što nam svaki put garantira novog prostog djelitelja. Budući da možemo zaključiti da proizvoljno velik broj dijeli
što nam svaki put garantira novog prostog djelitelja. Budući da možemo zaključiti da proizvoljno velik broj dijeli  ,
,  u ovom slučaju ne postoji.
u ovom slučaju ne postoji.Rješenja su
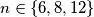 .
.  Školjka
Školjka  and
and  of
of 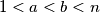 , the number
, the number 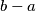 divides
divides