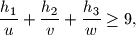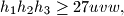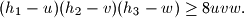Točno
27. ožujka 2016. 10:12 (9 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ako oznacimo sa  ,
, 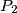 ,
, 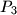 redom dvostruke povrsine trokuta
redom dvostruke povrsine trokuta 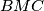 ,
, 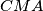 i
i 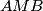 a sa
a sa  dvostruku povrsinu trokuta
dvostruku povrsinu trokuta  vrijedi
vrijedi
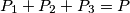 koristit cemo
koristit cemo 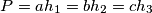
 ...
... 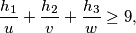
prosirivanjem prvog razlomka sa drugog sa
drugog sa  treceg sa
treceg sa  dobivamo
dobivamo
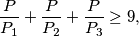
izlucivannjem i koristenjem
i koristenjem 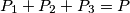 dobivamo
dobivamo
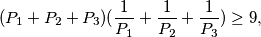 sto vrijedi zbog A-H nejednakosti
sto vrijedi zbog A-H nejednakosti
 ...
... 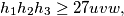 mnozenjem sa
mnozenjem sa 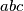 dobivamo
dobivamo
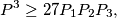 sada izvadimo
sada izvadimo  korjen i dobijemo
korjen i dobijemo
![\displaystyle P_1+P_2+P_3=P \geq 3 \cdot \sqrt[3]{P_1 P_2 P_3}](/media/m/4/d/d/4dde0c8d009c60f019ded63f909aeea7.png) a ovo vrijedi po A-G nejednakosti
a ovo vrijedi po A-G nejednakosti
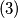 ...
... 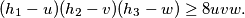 nakon sto sve izmnozimo i prebacimo sve na stranu na kojoj je pozitivno dobijemo
nakon sto sve izmnozimo i prebacimo sve na stranu na kojoj je pozitivno dobijemo
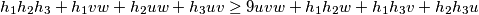
sada koristenjem po A-G nejednakosti vrijedi
po A-G nejednakosti vrijedi
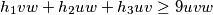
pa moramo samo pokazati
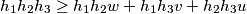
mozenjem sa dobivamo
dobivamo
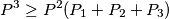 gdje cak vrijedi jednakost zbog
gdje cak vrijedi jednakost zbog 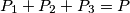
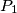 ,
, 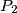 ,
, 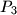 redom dvostruke povrsine trokuta
redom dvostruke povrsine trokuta 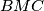 ,
, 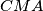 i
i 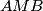 a sa
a sa  dvostruku povrsinu trokuta
dvostruku povrsinu trokuta  vrijedi
vrijedi 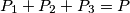 koristit cemo
koristit cemo 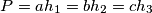
 ...
... 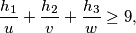
prosirivanjem prvog razlomka sa
 drugog sa
drugog sa  treceg sa
treceg sa  dobivamo
dobivamo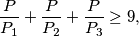
izlucivannjem
 i koristenjem
i koristenjem 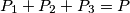 dobivamo
dobivamo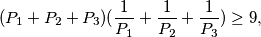 sto vrijedi zbog A-H nejednakosti
sto vrijedi zbog A-H nejednakosti ...
... 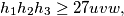 mnozenjem sa
mnozenjem sa  dobivamo
dobivamo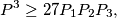 sada izvadimo
sada izvadimo  korjen i dobijemo
korjen i dobijemo![\displaystyle P_1+P_2+P_3=P \geq 3 \cdot \sqrt[3]{P_1 P_2 P_3}](/media/m/4/d/d/4dde0c8d009c60f019ded63f909aeea7.png) a ovo vrijedi po A-G nejednakosti
a ovo vrijedi po A-G nejednakosti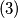 ...
... 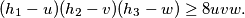 nakon sto sve izmnozimo i prebacimo sve na stranu na kojoj je pozitivno dobijemo
nakon sto sve izmnozimo i prebacimo sve na stranu na kojoj je pozitivno dobijemo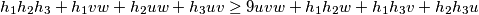
sada koristenjem
 po A-G nejednakosti vrijedi
po A-G nejednakosti vrijedi 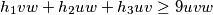
pa moramo samo pokazati
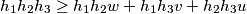
mozenjem sa
 dobivamo
dobivamo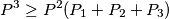 gdje cak vrijedi jednakost zbog
gdje cak vrijedi jednakost zbog 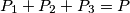
 Školjka
Školjka 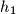 ,
, 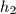 ,
, 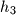 duljine visina trokuta
duljine visina trokuta  ,
,  ,
,  , redom, a
, redom, a  ,
,  ,
,  udaljenosti točke
udaljenosti točke  iz unutrašnjosti trokuta od stranica
iz unutrašnjosti trokuta od stranica