Točno
28. ožujka 2016. 13:34 (9 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Idemo na dokaz kontradikcijom. Traži se da pokažemo kako postoji 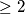 parnih brojeva, mi ćemo pokazati da ne može postojati
parnih brojeva, mi ćemo pokazati da ne može postojati 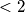 parnih brojeva iz čega direktno slijedi tvrdnja zadatka.
parnih brojeva iz čega direktno slijedi tvrdnja zadatka.
Tada razlikujemo dva slučaja
1) svi brojevi su neparni, tj. 0 parnih
tada za svaki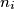 postoji
postoji 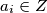 takav da
takav da 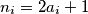
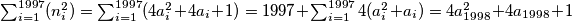
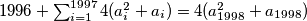
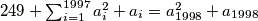
kvadrat nekog broja je iste parnosti kao i taj broj pa im je zbroj uvijek paran, slijedi
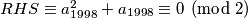
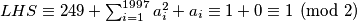
slijedi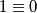 pa imamo kontradikciju
pa imamo kontradikciju
2) jedan broj je paran
imamo dva podslučaja, paran broj može biti na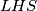 i na
i na 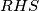
2.1) paran broj na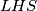
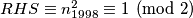
Na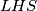 imamo tada 1996 neparnih brojeva i 1 paran. Pošto neparnih brojeva ima parno tj.
imamo tada 1996 neparnih brojeva i 1 paran. Pošto neparnih brojeva ima parno tj. 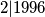 , zbroj im je paran. Slijedi da je zbroj 1996 neparnih i 1 parnog isti
, zbroj im je paran. Slijedi da je zbroj 1996 neparnih i 1 parnog isti 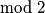 kao i zbroj parnog i parnog što je paran broj tj.
kao i zbroj parnog i parnog što je paran broj tj. 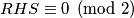
slijedi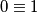 pa imamo kontradikciju i zaključujemo da je ovaj podslučaj nemoguć
pa imamo kontradikciju i zaključujemo da je ovaj podslučaj nemoguć
2.2) paran broj na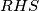
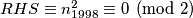
Na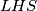 imamo zbroj 1997 neparnih, koji je neparan jer je broj neparnih brojeva u zbroju (1997) neparan tj.
imamo zbroj 1997 neparnih, koji je neparan jer je broj neparnih brojeva u zbroju (1997) neparan tj. 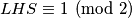
slijedi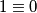 pa zaključujemo da je i ovaj podslučaj nemoguć te smo gotovi.
pa zaključujemo da je i ovaj podslučaj nemoguć te smo gotovi.
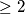 parnih brojeva, mi ćemo pokazati da ne može postojati
parnih brojeva, mi ćemo pokazati da ne može postojati 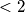 parnih brojeva iz čega direktno slijedi tvrdnja zadatka.
parnih brojeva iz čega direktno slijedi tvrdnja zadatka.Tada razlikujemo dva slučaja
1) svi brojevi su neparni, tj. 0 parnih
tada za svaki
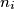 postoji
postoji 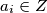 takav da
takav da 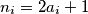
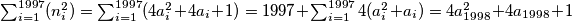
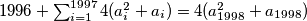
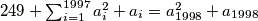
kvadrat nekog broja je iste parnosti kao i taj broj pa im je zbroj uvijek paran, slijedi
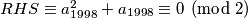
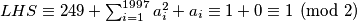
slijedi
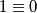 pa imamo kontradikciju
pa imamo kontradikciju2) jedan broj je paran
imamo dva podslučaja, paran broj može biti na
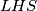 i na
i na 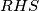
2.1) paran broj na
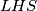
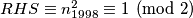
Na
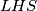 imamo tada 1996 neparnih brojeva i 1 paran. Pošto neparnih brojeva ima parno tj.
imamo tada 1996 neparnih brojeva i 1 paran. Pošto neparnih brojeva ima parno tj. 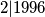 , zbroj im je paran. Slijedi da je zbroj 1996 neparnih i 1 parnog isti
, zbroj im je paran. Slijedi da je zbroj 1996 neparnih i 1 parnog isti 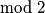 kao i zbroj parnog i parnog što je paran broj tj.
kao i zbroj parnog i parnog što je paran broj tj. 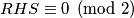
slijedi
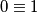 pa imamo kontradikciju i zaključujemo da je ovaj podslučaj nemoguć
pa imamo kontradikciju i zaključujemo da je ovaj podslučaj nemoguć2.2) paran broj na
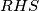
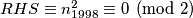
Na
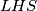 imamo zbroj 1997 neparnih, koji je neparan jer je broj neparnih brojeva u zbroju (1997) neparan tj.
imamo zbroj 1997 neparnih, koji je neparan jer je broj neparnih brojeva u zbroju (1997) neparan tj. 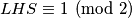
slijedi
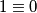 pa zaključujemo da je i ovaj podslučaj nemoguć te smo gotovi.
pa zaključujemo da je i ovaj podslučaj nemoguć te smo gotovi.  Školjka
Školjka 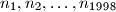 be positive integers such that
be positive integers such that 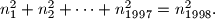 Show that at least two of the numbers are even.
Show that at least two of the numbers are even.