Točno
1. travnja 2016. 20:51 (9 godine, 10 mjeseci)
Find all ordered pairs
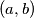
of positive integers for which the numbers
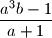
and
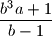
are both positive integers.
%V0
Find all ordered pairs $(a,b)$ of positive integers for which the numbers $\dfrac{a^3b-1}{a+1}$ and $\dfrac{b^3a+1}{b-1}$ are both positive integers.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
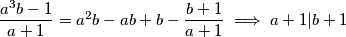
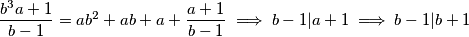

je djelitelj od
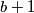
pa, pošto
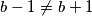
, slijedi
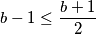
ili sređivanjem
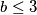
pa promatramo mogućnosti
1)
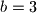
U tom slučaju
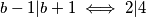
što vrijedi
također
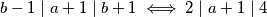
pa gledamo mogućnosti za

1.1)
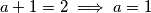
pa provjerom imamo uređen par
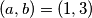
kao jedno rješenje
1.2)
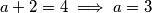
pa provjerom imamo
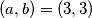
kao još jedno rješenje
2)

U tom slučaju
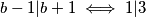
što vrijedi
također
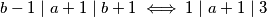
pa gledamo mogućnosti za

2.1)
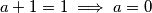
što je nemoguće jer
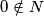
2.2)
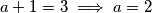
pa provjerom imamo
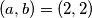
kao rješenje
3)
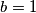
što je nemoguće jer tada u
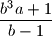
imamo

kao nazivnik
Sva moguća rješenja su uređeni parovi
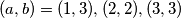
%V0
$ \dfrac{a^3b-1}{a+1} = a^2b - ab + b - \dfrac{b+1}{a+1} \implies a+1 | b+1$
$ \dfrac{b^3a+1}{b-1} = ab^2 + ab + a + \dfrac{a+1}{b-1} \implies b-1 | a+1 \implies b-1 | b +1$
$b-1$ je djelitelj od $b+1$ pa, pošto $b-1 \neq b+1$, slijedi $b-1 \leq \dfrac{b+1}{2}$ ili sređivanjem $b \leq 3$ pa promatramo mogućnosti
1) $b=3$
U tom slučaju $b-1|b+1 \iff 2|4$ što vrijedi
također $b-1\mid a+1\mid b+1 \iff 2 \mid a+1 \mid 4$ pa gledamo mogućnosti za $a$
1.1) $a + 1 = 2 \implies a = 1$ pa provjerom imamo uređen par $(a,b) = (1, 3)$ kao jedno rješenje
1.2) $a + 2= 4 \implies a = 3$ pa provjerom imamo $(a,b) = (3,3)$ kao još jedno rješenje
2) $b=2$
U tom slučaju $b-1|b+1 \iff 1|3$ što vrijedi
također $b-1\mid a+1\mid b+1 \iff 1 \mid a+1 \mid 3$ pa gledamo mogućnosti za $a$
2.1) $a + 1 = 1 \implies a = 0$ što je nemoguće jer $0 \notin N$
2.2) $a + 1 = 3 \implies a = 2$ pa provjerom imamo $(a,b) = (2,2)$ kao rješenje
3) $b=1$ što je nemoguće jer tada u $\dfrac{b^3a+1}{b-1}$ imamo $0$ kao nazivnik
Sva moguća rješenja su uređeni parovi $(a,b) = (1,3), (2,2), (3,3)$
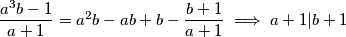
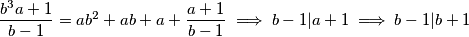
 je djelitelj od
je djelitelj od 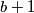 pa, pošto
pa, pošto 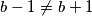 , slijedi
, slijedi 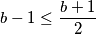 ili sređivanjem
ili sređivanjem 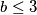 pa promatramo mogućnosti
pa promatramo mogućnosti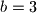
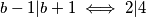 što vrijedi
što vrijedi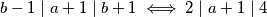 pa gledamo mogućnosti za
pa gledamo mogućnosti za 
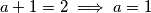 pa provjerom imamo uređen par
pa provjerom imamo uređen par 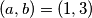 kao jedno rješenje
kao jedno rješenje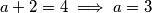 pa provjerom imamo
pa provjerom imamo 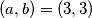 kao još jedno rješenje
kao još jedno rješenje
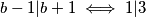 što vrijedi
što vrijedi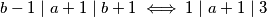 pa gledamo mogućnosti za
pa gledamo mogućnosti za 
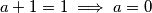 što je nemoguće jer
što je nemoguće jer 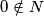
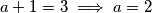 pa provjerom imamo
pa provjerom imamo 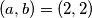 kao rješenje
kao rješenje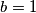 što je nemoguće jer tada u
što je nemoguće jer tada u 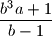 imamo
imamo  kao nazivnik
kao nazivnik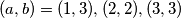
 Školjka
Školjka 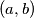 of positive integers for which the numbers
of positive integers for which the numbers 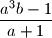 and
and