Točno
3. travnja 2016. 12:51 (8 godine, 8 mjeseci)
Nađite sve
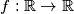
takve da je
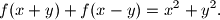
%V0
Nađite sve $f : \mathbb{R} \rightarrow \mathbb{R}$ takve da je $$f(x + y) + f(x - y) = x^2 + y^2\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uvrštavanjem
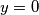
u funkciju
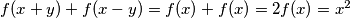
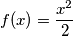
provjera:
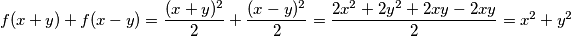
%V0
Uvrštavanjem $y=0$ u funkciju
$f(x + y) + f(x - y) = f(x) + f(x) = 2f(x) = x^2$
$f(x) = \dfrac{x^2}{2}$
provjera:
$f(x + y) + f(x - y) = \dfrac{(x+y)^2}{2} + \dfrac{(x-y)^2}{2} = \dfrac{2x^2 + 2y^2 +2xy -2xy}{2} = x^2+y^2$
| 3. travnja 2016. 15:32 | ikicic | Točno |
Školjka