Točno
10. travnja 2016. 16:28 (9 godine, 11 mjeseci)
Neka je
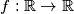
takva da je
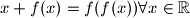
. Nađite sve

takve da
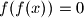
.
%V0
Neka je $f : \mathbb{R} \rightarrow \mathbb{R}$ takva da je $x + f(x)=f(f(x)) \forall x \in \mathbb{R}$. Nađite sve $x$ takve da $f(f(x))=0$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je
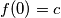
. Uvrštavanjem
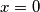
u uvjet dobijemo
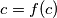
. Uvrstimo li sada

umjesto

u uvjet, imamo:
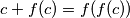
Odnosno:
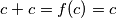
Pa je
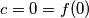
. Neka broj

zadovoljava
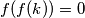
. Vrijedi
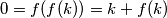
te je iz toga
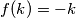
. Sada je:
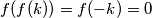
Te nakon što uzmemo funkciju lijeve i desne strane:
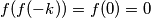
Zbog uvjeta zadatka imamo
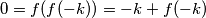
pa je
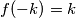
, ali već smo dobili da je
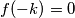
pa zaključujemo da mora biti
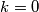
.
%V0
Neka je $f(0)=c$. Uvrštavanjem $x=0$ u uvjet dobijemo $c=f(c)$. Uvrstimo li sada $c$ umjesto $x$ u uvjet, imamo:
$$c+f(c)=f(f(c))$$
Odnosno:
$$c+c=f(c)=c$$
Pa je $c=0=f(0)$. Neka broj $k$ zadovoljava $f(f(k))=0$. Vrijedi $0=f(f(k))=k+f(k)$ te je iz toga $f(k)=-k$. Sada je:
$$f(f(k))=f(-k)=0$$
Te nakon što uzmemo funkciju lijeve i desne strane:
$$f(f(-k))=f(0)=0$$
Zbog uvjeta zadatka imamo $0=f(f(-k))=-k+f(-k)$ pa je $f(-k)=k$, ali već smo dobili da je $f(-k)=0$ pa zaključujemo da mora biti $k=0$.
| 10. travnja 2016. 16:50 | ikicic | Točno |