Točno
17. travnja 2016. 12:19 (9 godine, 9 mjeseci)
Veoma dobro poznata je nejednakost trokuta, koja govori da u svakom trokutu sa stranicama

vrijedi
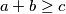
,
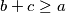
,
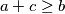
pri kojoj se jednakost postiže u degeneriranim trokutima.
Dokažite jaču nejednakost
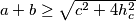
,
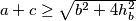
,
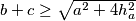
gdje su
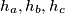
visine na stranice

. Kada se postiže jednakost?
%V0
Veoma dobro poznata je nejednakost trokuta, koja govori da u svakom trokutu sa stranicama $a, b, c$ vrijedi $a+b\geq c$, $b+c\geq a$, $a+c \geq b$ pri kojoj se jednakost postiže u degeneriranim trokutima.
Dokažite jaču nejednakost $a+b \geq \sqrt{c^2+4h_c^2}$, $a+c \geq \sqrt{b^2+4h_b^2}$, $b+c \geq \sqrt{a^2+4h_a^2}$ gdje su $h_a, h_b, h_c$ visine na stranice $a, b, c$. Kada se postiže jednakost?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.

Primjetimo da je
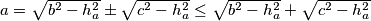
Prema tome,
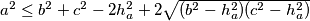
Nadalje,
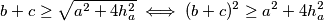
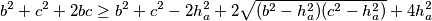
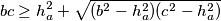
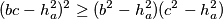
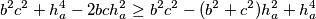
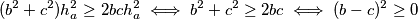
Što dokazuje originalnu nejednakost.
Jednakost može vrijediti samo ako
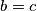
ili
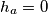
te provjerom dobivamo da u jednakokračnim i degeneriranim trokutima jednakost uistinu vrijedi.
Analogno provodimo dokaz za druge dvije stranice.

Neka su stranice

nasuprotne vrhovima
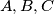
i neka je

nožište visine iz vrha

na stranicu

.
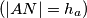
Neka je

točka takva da je
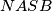
pravokutnik. Neka je

točka na na polupravcu

takva da
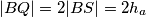
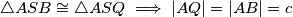
pa po nejednakosti trokuta na
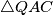
mora vrijediti
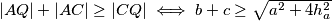
Jednakost se postiže kada
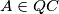
a tada
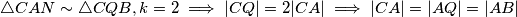
pa je

jednakokračan.
Lako je vidjeti da se jednakost postiže i kada je

degeneriran.
Analogno provodimo dokaz za druge dvije stranice.
%V0
$(1)$
Primjetimo da je $a = \sqrt{b^2-h_a^2} \pm \sqrt{c^2-h_a^2} \leq \sqrt{b^2-h_a^2} + \sqrt{c^2-h_a^2}$
Prema tome, $a^2 \leq b^2+c^2-2h_a^2 +2\sqrt{(b^2-h_a^2)(c^2-h_a^2)}$
Nadalje,
$$b+c \geq \sqrt{a^2+4h_a^2} \iff (b+c)^2 \geq a^2 + 4h_a^2 $$
$$b^2 + c^2 + 2bc \geq b^2 + c^2 - 2h_a^2 + 2\sqrt{(b^2 - h_a^2)(c^2 - h_a^2)} + 4h_a^2$$
$$bc \geq h_a^2 + \sqrt{(b^2 - h_a^2)(c^2 - h_a^2)}$$
$$(bc-h_a^2)^2 \geq (b^2 - h_a^2)(c^2 - h_a^2)$$
$$b^2c^2 + h_a^4 - 2bch_a^2 \geq b^2c^2 - (b^2+c^2)h_a^2 + h_a^4$$
$$(b^2+c^2)h_a^2 \geq 2bch_a^2 \iff b^2 +c^2 \geq 2bc \iff (b-c)^2 \geq 0$$
Što dokazuje originalnu nejednakost.
Jednakost može vrijediti samo ako $b = c$ ili $h_a = 0$ te provjerom dobivamo da u jednakokračnim i degeneriranim trokutima jednakost uistinu vrijedi.
Analogno provodimo dokaz za druge dvije stranice.
$(2)$
Neka su stranice $a, b, c$ nasuprotne vrhovima $A, B, C$ i neka je $N$ nožište visine iz vrha $A$ na stranicu $a$. $(|AN| = h_a)$
Neka je $S$ točka takva da je $NASB$ pravokutnik. Neka je $Q$ točka na na polupravcu $BS$ takva da $|BQ| = 2|BS| = 2h_a$
$\triangle ASB \cong \triangle ASQ \implies |AQ| = |AB| = c$ pa po nejednakosti trokuta na $\triangle QAC$ mora vrijediti $|AQ| + |AC| \geq |CQ| \iff b + c \geq \sqrt{a^2 +4h_a^2}$
Jednakost se postiže kada $A \in QC$ a tada $\triangle CAN \sim \triangle CQB, k = 2 \implies |CQ| = 2|CA| \implies |CA| = |AQ| = |AB| $ pa je $\triangle ABC$ jednakokračan.
Lako je vidjeti da se jednakost postiže i kada je $\triangle ABC$ degeneriran.
Analogno provodimo dokaz za druge dvije stranice.
| 4. svibnja 2016. 14:24 | grga | Točno |

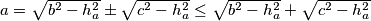
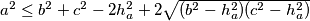
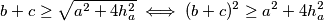
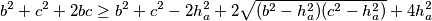
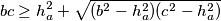
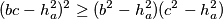
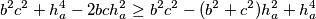
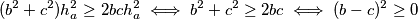
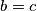 ili
ili 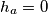 te provjerom dobivamo da u jednakokračnim i degeneriranim trokutima jednakost uistinu vrijedi.
te provjerom dobivamo da u jednakokračnim i degeneriranim trokutima jednakost uistinu vrijedi. 
 nasuprotne vrhovima
nasuprotne vrhovima 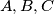 i neka je
i neka je  nožište visine iz vrha
nožište visine iz vrha  na stranicu
na stranicu  .
. 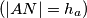
 točka takva da je
točka takva da je 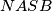 pravokutnik. Neka je
pravokutnik. Neka je  točka na na polupravcu
točka na na polupravcu  takva da
takva da 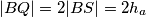
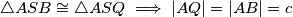 pa po nejednakosti trokuta na
pa po nejednakosti trokuta na 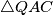 mora vrijediti
mora vrijediti 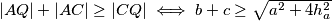
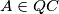 a tada
a tada 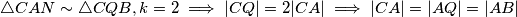 pa je
pa je  jednakokračan.
jednakokračan. degeneriran.
degeneriran. Školjka
Školjka 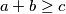 ,
, 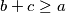 ,
, 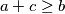 pri kojoj se jednakost postiže u degeneriranim trokutima.
pri kojoj se jednakost postiže u degeneriranim trokutima.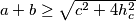 ,
, 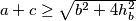 ,
, 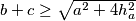 gdje su
gdje su 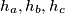 visine na stranice
visine na stranice