Točno
9. lipnja 2016. 15:02 (9 godine, 9 mjeseci)
Korisnik: nixy123
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Zadatak: Simulacija općinskog 2016. za prvi razred zadatak 1. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
ikicic, 9. lipnja 2016. 21:26
Mala preporuka, iako je mrvicu kompliciranije, matematičke izraze je dobro pisati koristeći LaTeX.
Primjerice, prvi red se može preglednije zapisati pomoću
$a^2 b^2 c^2 \frac{1}{a^3} + \frac{1}{b^3} + \frac{1}{c^3} = a^3 + b^3 + c^3$
što daje
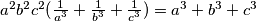
Dakle, matematičke formule treba pisati unutar $ ... $.
Npr:
$a^2$ -->
$\frac{x}{y}$ -->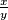
$a + (b + c)$ -->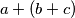
Nešto više detalja ovdje.
Inače, rješenje je O.K.
Primjerice, prvi red se može preglednije zapisati pomoću
$a^2 b^2 c^2 \frac{1}{a^3} + \frac{1}{b^3} + \frac{1}{c^3} = a^3 + b^3 + c^3$
što daje
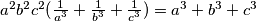
Dakle, matematičke formule treba pisati unutar $ ... $.
Npr:
$a^2$ -->

$\frac{x}{y}$ -->
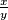
$a + (b + c)$ -->
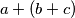
Nešto više detalja ovdje.
Inače, rješenje je O.K.
 Školjka
Školjka 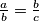 , gdje su
, gdje su  realni brojevi različiti od nule. Dokažite da tada vrijedi:
realni brojevi različiti od nule. Dokažite da tada vrijedi: