Točno
22. lipnja 2016. 13:49 (9 godine, 8 mjeseci)
Let
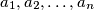
be positive real numbers such that
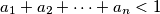
. Prove that
![\frac{a_{1} a_{2} \cdots a_{n} \left[ 1 - (a_{1} + a_{2} + \cdots + a_{n}) \right] }{(a_{1} + a_{2} + \cdots + a_{n})( 1 - a_1)(1 - a_2) \cdots (1 - a_n)} \leqslant \frac{1}{n^{n+1}}](/media/m/0/b/a/0bab773e1ec6962f3cabbe1b3882b9ff.png)
%V0
Let $a_{1},a_{2},\ldots ,a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots +a_{n}<1$. Prove that
$$\frac{a_{1} a_{2} \cdots a_{n} \left[ 1 - (a_{1} + a_{2} + \cdots + a_{n}) \right] }{(a_{1} + a_{2} + \cdots + a_{n})( 1 - a_1)(1 - a_2) \cdots (1 - a_n)} \leqslant \frac{1}{n^{n+1}}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Po uvjetima zadatka možemo uvesti novi član
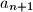
tako da je
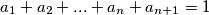
. Neka je

umnožak svih tih brojeva.
Tada traženu nejednakost možemo zapisati kao
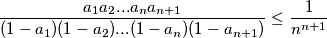
.
Po
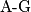
nejednakosti vrijedi da je
![\frac{a_1}{1-a_1}=\frac{a_1}{a_2+a_3+...+a_n+a_{n+1}} \leq \frac{a_1}{n \sqrt[n]{\frac{P}{a_1}}}](/media/m/e/0/1/e016d5b53507a0189225a470c417d3df.png)
.
Množenjem svih tih nejednakosti je:
![LHS \leq \frac{P}{n^{n+1} \sqrt[n]{\frac{P^{n+1}}{P}}}=\frac{P}{n^{n+1}P}=\frac{1}{n^{n+1}}](/media/m/e/4/3/e43aa24631a83830899c541670ae8e0e.png)
što je i trebalo dokazati.
%V0
Po uvjetima zadatka možemo uvesti novi član $a_{n+1}$ tako da je $a_1+a_2+...+a_n+a_{n+1}=1$. Neka je $P$ umnožak svih tih brojeva.
Tada traženu nejednakost možemo zapisati kao
$$\frac{a_1 a_2 ... a_n a_{n+1}}{(1-a_1)(1-a_2)...(1-a_n)(1-a_{n+1})}\leq\frac{1}{n^{n+1}}$$.
Po $\text{A-G}$ nejednakosti vrijedi da je $\frac{a_1}{1-a_1}=\frac{a_1}{a_2+a_3+...+a_n+a_{n+1}} \leq \frac{a_1}{n \sqrt[n]{\frac{P}{a_1}}}$.
Množenjem svih tih nejednakosti je:
$$LHS \leq \frac{P}{n^{n+1} \sqrt[n]{\frac{P^{n+1}}{P}}}=\frac{P}{n^{n+1}P}=\frac{1}{n^{n+1}}$$
što je i trebalo dokazati.
| 22. lipnja 2016. 21:11 | ikicic | Točno |