Točno
23. lipnja 2016. 00:58 (9 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pokušat ćemo tvrdnju zadatka dokazati Cauchyevom indukcijom:
Baza: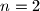
Imamo:
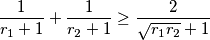
ali lako se možemo uvjeriti (oduzimanjem desne strane od lijeve) da:
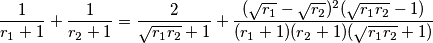
što očito dokazuje gore navedenu nejednakost za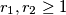
Pretpostavka: za neki vrijedi:
vrijedi:
![\sum_{i=1}^{n} \frac{1}{r_{i} + 1} \geq \frac{n}{ \sqrt[n]{r_{1} \cdots r_{n}}+1}](/media/m/9/2/a/92adfde36c366097f34bfc4eb78ed089.png)
Korak: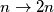
Imamo:
![\sum_{i=1}^{2n} \frac{1}{r_{i} + 1} = \sum_{i=1}^{n} \frac{1}{r_{i} + 1} + \sum_{i=n+1}^{2n} \frac{1}{r_{i} + 1} \geq n \cdot\Bigg(\frac{1}{ \sqrt[n]{r_{1} \cdots r_{n}}+1}+\frac{1}{ \sqrt[n]{r_{n+1} \cdots r_{2n}}+1}\Bigg) \geq \frac{2n}{\sqrt[2n]{r_1\cdots r_{2n}}+1}](/media/m/a/9/9/a99cc9359ec55c155452c0ccc2693425.png)
Čime je korak dokazan.
Korak: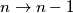
Uzmimo:![r_n = \sqrt[n-1]{r_1\cdots r_{n-1}}](/media/m/6/a/a/6aa91d10cad79eb39cada4d8d8234b51.png)
Tada imamo:
![\frac{1}{ \sqrt[n-1]{r_1\cdots r_{n-1}}+1}+\sum_{i=1}^{n-1} \frac{1}{r_{i} + 1} \geq \frac{n}{ (r_{1} \cdots r_{n-1}\cdot (r_{1} \cdots r_{n-1})^\frac{1}{n-1})^{\frac{1}{n}}+1}= \frac{n}{(((r_{1} \cdots r_{n-1})^{\frac{n}{n-1}})^{\frac{1}{n}}+1} = \frac{n-1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1} + \frac{1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1}](/media/m/f/d/f/fdf754a6a1bea50c37b0b6e6945903aa.png)
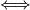
![\sum_{i=1}^{n-1} \frac{1}{r_{i} + 1} \geq \frac{n-1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1}](/media/m/7/f/d/7fdc56218dd193882ee93116586ae741.png)
Čime je korak dokazan.
Po pretpostavci matematičke indukcije, tvrdnja zadatka vrijedi za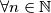 .
.
Baza:
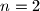
Imamo:
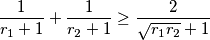
ali lako se možemo uvjeriti (oduzimanjem desne strane od lijeve) da:
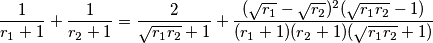
što očito dokazuje gore navedenu nejednakost za
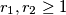
Pretpostavka: za neki
 vrijedi:
vrijedi:![\sum_{i=1}^{n} \frac{1}{r_{i} + 1} \geq \frac{n}{ \sqrt[n]{r_{1} \cdots r_{n}}+1}](/media/m/9/2/a/92adfde36c366097f34bfc4eb78ed089.png)
Korak:
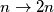
Imamo:
![\sum_{i=1}^{2n} \frac{1}{r_{i} + 1} = \sum_{i=1}^{n} \frac{1}{r_{i} + 1} + \sum_{i=n+1}^{2n} \frac{1}{r_{i} + 1} \geq n \cdot\Bigg(\frac{1}{ \sqrt[n]{r_{1} \cdots r_{n}}+1}+\frac{1}{ \sqrt[n]{r_{n+1} \cdots r_{2n}}+1}\Bigg) \geq \frac{2n}{\sqrt[2n]{r_1\cdots r_{2n}}+1}](/media/m/a/9/9/a99cc9359ec55c155452c0ccc2693425.png)
Čime je korak dokazan.
Korak:
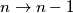
Uzmimo:
![r_n = \sqrt[n-1]{r_1\cdots r_{n-1}}](/media/m/6/a/a/6aa91d10cad79eb39cada4d8d8234b51.png)
Tada imamo:
![\frac{1}{ \sqrt[n-1]{r_1\cdots r_{n-1}}+1}+\sum_{i=1}^{n-1} \frac{1}{r_{i} + 1} \geq \frac{n}{ (r_{1} \cdots r_{n-1}\cdot (r_{1} \cdots r_{n-1})^\frac{1}{n-1})^{\frac{1}{n}}+1}= \frac{n}{(((r_{1} \cdots r_{n-1})^{\frac{n}{n-1}})^{\frac{1}{n}}+1} = \frac{n-1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1} + \frac{1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1}](/media/m/f/d/f/fdf754a6a1bea50c37b0b6e6945903aa.png)
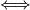
![\sum_{i=1}^{n-1} \frac{1}{r_{i} + 1} \geq \frac{n-1}{\sqrt[n-1]{r_1\cdots r_{n-1}}+1}](/media/m/7/f/d/7fdc56218dd193882ee93116586ae741.png)
Čime je korak dokazan.
Po pretpostavci matematičke indukcije, tvrdnja zadatka vrijedi za
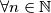 .
.  Školjka
Školjka 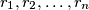 be real numbers greater than or equal to 1. Prove that
be real numbers greater than or equal to 1. Prove that ![\frac{1}{r_{1} + 1} + \frac{1}{r_{2} + 1} + \cdots +\frac{1}{r_{n}+1} \geq \frac{n}{ \sqrt[n]{r_{1}r_{2} \cdots r_{n}}+1}.](/media/m/6/5/9/659a1db9dfb0819c970e78fed531b4ad.png)