Točno
23. lipnja 2016. 22:32 (9 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ako je 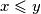 ,tada je
,tada je 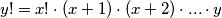 , pa možemo i reći da
, pa možemo i reći da 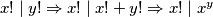 .
.
Sad za svaki prost broj iz skupa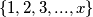 kao djelitelj
kao djelitelj 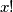 vrijedi da je djelitelj
vrijedi da je djelitelj 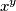 , a kako je prost i samog
, a kako je prost i samog 
 .
.  Trivijalno je uvidjeti da svaki prost djelitelj
Trivijalno je uvidjeti da svaki prost djelitelj  mora biti manji ili jednak
mora biti manji ili jednak 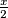 .
.
S druge strane po oslabljenoj verziji Bertrandovog postulata (za koji sam totalno znao i prije ovog) vrijedi da za svaki prirodan broj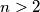 postoji barem jedan prost broj
postoji barem jedan prost broj  za koji vrijedi
za koji vrijedi 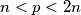 .
.
Taj prost broj po mora biti djelitelj
mora biti djelitelj  , što je nemoguće po
, što je nemoguće po  . Dakle, ne postoji rješenje za
. Dakle, ne postoji rješenje za 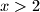 . Preostaje proučiti slučajeve kad je
. Preostaje proučiti slučajeve kad je 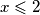 . Ovdje dobivamo jedina rješenja
. Ovdje dobivamo jedina rješenja 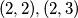 .
.
Ako je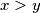 tada se analogno dolazi do
tada se analogno dolazi do 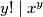 pa i
pa i 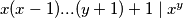 . S druge strane
. S druge strane 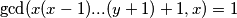 , pa ovdje nema rješenja.
, pa ovdje nema rješenja.
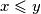 ,tada je
,tada je 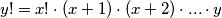 , pa možemo i reći da
, pa možemo i reći da 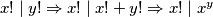 .
.Sad za svaki prost broj iz skupa
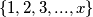 kao djelitelj
kao djelitelj 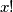 vrijedi da je djelitelj
vrijedi da je djelitelj 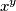 , a kako je prost i samog
, a kako je prost i samog 
 .
.  Trivijalno je uvidjeti da svaki prost djelitelj
Trivijalno je uvidjeti da svaki prost djelitelj  mora biti manji ili jednak
mora biti manji ili jednak 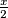 .
.S druge strane po oslabljenoj verziji Bertrandovog postulata (za koji sam totalno znao i prije ovog) vrijedi da za svaki prirodan broj
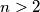 postoji barem jedan prost broj
postoji barem jedan prost broj  za koji vrijedi
za koji vrijedi 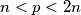 .
.Taj prost broj po
 mora biti djelitelj
mora biti djelitelj  , što je nemoguće po
, što je nemoguće po  . Dakle, ne postoji rješenje za
. Dakle, ne postoji rješenje za 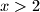 . Preostaje proučiti slučajeve kad je
. Preostaje proučiti slučajeve kad je 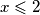 . Ovdje dobivamo jedina rješenja
. Ovdje dobivamo jedina rješenja 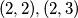 .
.Ako je
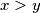 tada se analogno dolazi do
tada se analogno dolazi do 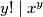 pa i
pa i 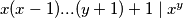 . S druge strane
. S druge strane 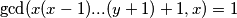 , pa ovdje nema rješenja.
, pa ovdje nema rješenja.  Školjka
Školjka  of positive integers satisfying the equation
of positive integers satisfying the equation 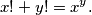
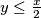 nego
nego 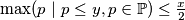 za Bertranda, pa ne možeš baš odmah dobiti kontradikciju.
za Bertranda, pa ne možeš baš odmah dobiti kontradikciju. 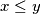 samo pretpostaviti za ovakav asimetričan izraz. Obrazloži.
samo pretpostaviti za ovakav asimetričan izraz. Obrazloži.