Točno
25. lipnja 2016. 22:28 (9 godine, 7 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Trivijalna lemma  : Ako za prirodne brojeve
: Ako za prirodne brojeve 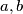 vrijedi
vrijedi 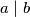 tada slijedi
tada slijedi 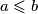 .
.
Uvrstimo sada te uz
te uz  dobijemo
dobijemo 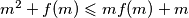 što je ekvivalentno
što je ekvivalentno 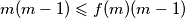 pa za
pa za 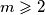 dobivamo
dobivamo 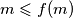 . Ako sada u početnu djeljivost uvrstimo
. Ako sada u početnu djeljivost uvrstimo 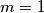 , lako se dobiva da i za
, lako se dobiva da i za  vrijedi
vrijedi 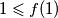 . Dakle za sve prirodne
. Dakle za sve prirodne  vrijedi
vrijedi 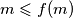 .
.
Uvrštavanjem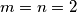 se dobiva
se dobiva 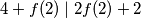 . Ako uzmemo
. Ako uzmemo 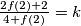 dobivamo
dobivamo 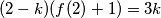 pa dobivamo
pa dobivamo 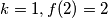 . Uvrstimo još
. Uvrstimo još  i opći
i opći  te dobivamo
te dobivamo 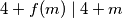 pa po
pa po  slijedi da je
slijedi da je 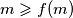 za svaki prirodni
za svaki prirodni  .
.
Kako je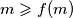 i
i 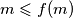 jedino je moguće da je
jedino je moguće da je 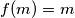 za svaki prirodni
za svaki prirodni  , što se uvrštavanjem potvrđuje kao rješenje.
, što se uvrštavanjem potvrđuje kao rješenje.
 : Ako za prirodne brojeve
: Ako za prirodne brojeve 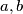 vrijedi
vrijedi 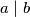 tada slijedi
tada slijedi 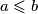 .
.Uvrstimo sada
 te uz
te uz  dobijemo
dobijemo 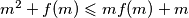 što je ekvivalentno
što je ekvivalentno 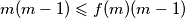 pa za
pa za 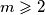 dobivamo
dobivamo 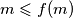 . Ako sada u početnu djeljivost uvrstimo
. Ako sada u početnu djeljivost uvrstimo 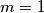 , lako se dobiva da i za
, lako se dobiva da i za  vrijedi
vrijedi 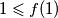 . Dakle za sve prirodne
. Dakle za sve prirodne  vrijedi
vrijedi 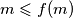 .
.Uvrštavanjem
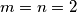 se dobiva
se dobiva 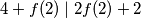 . Ako uzmemo
. Ako uzmemo 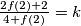 dobivamo
dobivamo 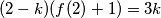 pa dobivamo
pa dobivamo 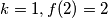 . Uvrstimo još
. Uvrstimo još  i opći
i opći  te dobivamo
te dobivamo 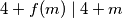 pa po
pa po  slijedi da je
slijedi da je 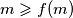 za svaki prirodni
za svaki prirodni  .
.Kako je
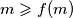 i
i 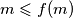 jedino je moguće da je
jedino je moguće da je 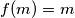 za svaki prirodni
za svaki prirodni  , što se uvrštavanjem potvrđuje kao rješenje.
, što se uvrštavanjem potvrđuje kao rješenje. Ocjene: (1)
Komentari:
grga, 22. srpnja 2016. 23:36
odlicno rjesenje, osim uz 2 tipfelera:
zapravo, ako uvrstis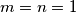 , dobit ces
, dobit ces 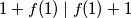 , iz cega se i neda nesto zakljuciti.
, iz cega se i neda nesto zakljuciti.
no naravno, cinjenica da je kodomena od skup prirodnih brojeva (koji se ovdje nimalo zbunjujuce oznacava sa "
skup prirodnih brojeva (koji se ovdje nimalo zbunjujuce oznacava sa "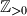 ") ima kao posljedicu
") ima kao posljedicu 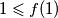 .
.
mislim da je tu uvrsteno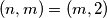 .
.
Ako sada u početnu djeljivost uvrstimo 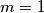 , lako se dobiva da i za
, lako se dobiva da i za  vrijedi
vrijedi 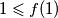
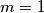 , lako se dobiva da i za
, lako se dobiva da i za  vrijedi
vrijedi 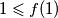
zapravo, ako uvrstis
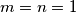 , dobit ces
, dobit ces 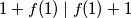 , iz cega se i neda nesto zakljuciti.
, iz cega se i neda nesto zakljuciti.no naravno, cinjenica da je kodomena od
 skup prirodnih brojeva (koji se ovdje nimalo zbunjujuce oznacava sa "
skup prirodnih brojeva (koji se ovdje nimalo zbunjujuce oznacava sa "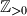 ") ima kao posljedicu
") ima kao posljedicu 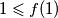 .
. Uvrstimo još  i opći
i opći  te dobivamo
te dobivamo 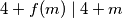
 i opći
i opći  te dobivamo
te dobivamo 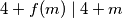
mislim da je tu uvrsteno
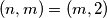 .
.  Školjka
Školjka 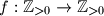 such that
such that 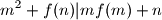 for all positive integers
for all positive integers  .
.